Расчеты на действие касательных и сжимающих напряжений (часть 2)
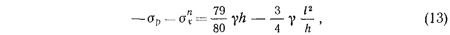
где σp — предел прочности твердеющей закладки на разрыв.
Из выражения (13) следует, что если ширина обнажения становится соизмеримой с высотой бруса, то растягивающие напряжения в нем исчезают. Если условие (13) не удовлетворяется, то в середине бруса образуется трещина, которая распространяется до некоторой точки с ординатой у1.
Сумма сжимающих напряжений Р в сжатой зоне в том его сечении, в котором возникла трещина, определяется с учетом появления дополнительных напряжений. Сумма моментов всех сил в рассматриваемом сечении относительно точки, в которой σx = 0, остается прежней, так как граничные условия в брусе при образовании трещины не изменяются. Момент же от равнодействующей растягивающих напряжений на участке — h/2≤ у ≤ у1 оказывается равным нулю.
В связи с тем, что прогиб бруса, возникший при появлении в нем трещины, бесконечно мал по сравнению с его высотой, то расположение и размеры зон сжатия и растяжения в рассматриваемом сечении можно считать неизменными.
В таком случае ординаты точек, в одной из которых кончается трещина у1 а во второй начинается зона сжатия у2, можно найти при решении уравнений
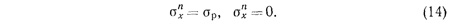
Левая часть уравнений представляет собой зависимость (10), а σp является пределом прочности твердеющей закладки на разрыв. Решив уравнения, получим
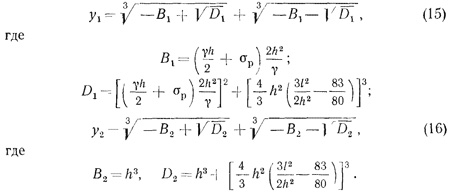
Сумма основных и дополнительных сжимающих напряжений h в брусе единичной ширины в сечении х = 0 на участке у2 ≤ у ≤ h/2 можно найти из уравнения моментов, имеющего вид
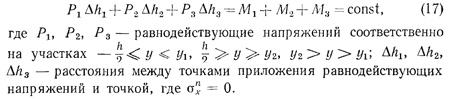
- Расчеты на действие касательных и сжимающих напряжений (часть 1)
- Системы разработки с нисходящей выемкой руды (часть 5)
- Системы разработки с нисходящей выемкой руды (часть 4)
- Системы разработки с нисходящей выемкой руды (часть 3)
- Системы разработки с нисходящей выемкой руды (часть 2)
- Системы разработки с нисходящей выемкой руды (часть 1)
- Система разработки со станковой крепью (часть 2)
- Система разработки со станковой крепью (часть 1)
- Системы разработки с восходящей выемкой руды слоями (часть 5)
- Системы разработки с восходящей выемкой руды слоями (часть 4)
- Системы разработки с восходящей выемкой руды слоями (часть 3)
- Системы разработки с восходящей выемкой руды слоями (часть 2)
- Системы разработки с восходящей выемкой руды слоями (часть 1)
- Системы разработки с креплением очистного пространства (V класс)
- Системы разработки с креплением очистного пространства (IV класс)
- Системы разработки с закладкой выработанного пространства (часть 4)
- Системы разработки с закладкой выработанного пространства (часть 3)
- Системы разработки с закладкой выработанного пространства (часть 2)
- Системы разработки с закладкой выработанного пространства (часть 1)
- Возведение бетонных настилов (часть 3)
- Возведение бетонных настилов (часть 2)
- Возведение бетонных настилов (часть 1)
- Очистные работы (часть 3)
- Очистные работы (часть 2)
- Очистные работы (часть 1)
- Система разработки горизонтальными слоями в восходящем порядке
- Системы разработки с закладкой очистного пространства (III класс)
- Конструкции погрузочных машин непрерывного действия (часть 2)
- Конструкции погрузочных машин непрерывного действия (часть 1)
- Конструкции погрузочных машин периодического действия (часть 4)

