Деформационные свойства горных пород (часть 1)

Горные породы под действием приложенных нагрузок в одних случаях меняют только свою форму и объем без разрыва сплошности (пластичная деформация), в других разрушаются на отдельные элементы без заметной пластичной деформации. В связи с этим выделяют такие важные свойства пород, как пластичность, хрупкость и упругость.
Пластичностью горных пород называется свойство горных пород в известных условиях и пределах под воздействием сил претерпевать остаточную деформацию (пластические деформации после снятия нагрузки) без микроскопических нарушений сплошности.
Пластичности обычно противопоставляется понятие хрупкость, т. е. способность горных пород под воздействием сил разрушаться без заметных пластических деформаций. Эти породы имеют слабую сопротивляемость разрушению при действии на нее ударной нагрузки. В породах с повышенной хрупкостью повышается эффект взрыва, но увеличиваются переборы по сечению, что приводит к лишним затратам при погрузке породы, креплении выработки и пр.
Упругость — способность породы восстанавливать первоначальную форму и объем после снятия нагрузки.
Проявление тех или иных свойств горных пород в значительной мере связано с условиями нагружения.
При мгновенном нагружении многие горные породы (песчаники, сланцы и др.) разрушаются на отдельные осколки, проявляя типичное свойство хрупкости. Вместе с тем эти же породы при постепенном нагружении ведут себя как упругие тела, т. е. пропорционально силам растут деформации. При длительном воздействии нагрузки в них проявляются остаточные деформации, т. е. породы проявляют пластичность.
Таким образом, упругость, хрупкость и пластичность имеют относительный характер.
Хрупкость и пластичность оцениваются коэффициентом пластичности (хрупкости), равным отношению общей работы деформации до разрушения Аобщ к работе упругой деформации Аупр, т. е. k = Аобщ/Аупр.
Хрупкое разрушение в чистом виде оценивается коэффициентом k=1. При пластических свойствах коэффициент к увеличивается.
Упругость твердых горных пород характеризуется: модулем упругости Е (модуль Юнга), коэффициентом Пуассона μ, модулем сдвига G. Кроме них иногда пользуются такими показателями, как модуль деформации Е0 и динамический модуль упругости Ед.
Модуль Юнга представляет собой отношение нормального напряжения σ к относительной деформации ξу.
Коэффициент Пуассона представляет собой отношение относительных деформаций — поперечной к продольной μ=ξ1у/ξу
Модуль Юнга и коэффициент Пуассона вычисляют по данным лабораторных испытаний пород.
Модуль сдвига по сложности его определения лабораторным путем может быть определен по формуле

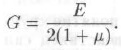
Модуль деформации есть отношение нормального напряжения к полной относительной деформации Еп, т. е. Е0=σ/Еп.

---