Горное давление. Напряженное состояние горных пород

Напряжения, возникающие в массиве горных пород, окружающих выработку, под действием силы собственного веса породы, тектонических сил и разности температур, называют горным давлением, а различные механические явления, происходящие в результате воздействия на горные породы этих напряжений, — проявлениями горного давления, которые могут быть в виде:
1) упругого или упруговязкого смещения пород без их разрушения;
2) вывалообразования (местного или регулярного) в слабых, трещиноватых и мелкослоистых породах;
3) разрушения и смещения пород (в частности, вывалообразования) под влиянием предельных напряжений в массиве по всему периметру сечения выработки или на отдельных его участках;
4) выдавливания пород в выработку вследствие пластического течения, в частности, со стороны почвы (пучение пород).
Напряженное состояние нетронутого массива, созданное гравитационными силами, является исходным силовым полем, в значительной степени предопределяющим поведение боковых пород в обнажениях при проведении подземных горных выработок.
В нетронутом массиве горных пород (до проведения выработок) имеет место равновесное объемное напряженное состояние. Обычно делается допущение, что напряжения обусловлены только плотностью толщи пород, а массив условно принимается как однородный и изотропный.
Рассмотрим напряженное состояние кубика со стороной, равной единице измерения (рис. 46), на глубине H(z) от поверхности.

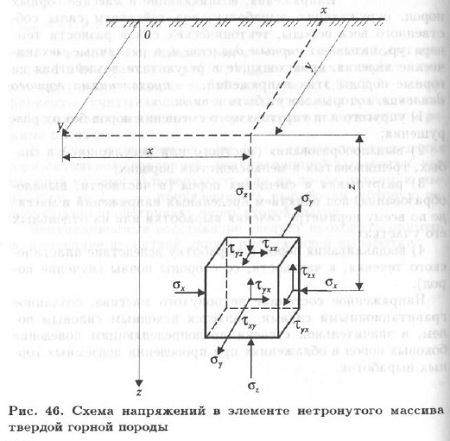
Он находится в условиях всестороннего сжатия, характеризующегося напряжениями σz, σx, σу. Поскольку среда принимается однородной, а оси координат произвольны, напряжения σx и σу равны. Вертикальная составляющая σz определяется массой столба породы единичной площади
высотой Н:

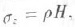
где ρ — плотность породы, т/м3.
Величину возможной деформации ξ в направлении осей можно определить по закону Гука, из которого абсолютное удлинение стержня

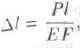
где Δl — абсолютное удлинение стержня от действия силы Л, м; l — длина стержня до воздействия силы Р, м; Е — модуль Юнга; F — площадь поперечного сечения стержня, м2.
Отношение Δl/l=ξy называется относительным продольным, а Δb/b=ξ' — относительным поперечным удлинением стержня. Отношение Р/F=σ, откуда ξy=σ/Е, где σ — нормальное напряжение, Н/м2. От действия сил происходят продольная и поперечная деформации кубика.
Суммарная деформация по осям х и z равна произведению

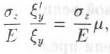
по осям x и у соответственно

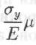
(здесь μ=ξ'у/ξy — коэффициент Пуассона).
По оси х произойдет только продольная деформация сжатия — σx/Е.
Полная относительная деформация по оси х

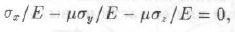
откуда при σу=σx получим уравнение напряжения в нетронутом массиве:

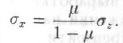
Отношение μ/(1 — μ)=λ называется коэффициентом бокового распора (обычно меньше 1).

---