Расчет горного давления в горизонтальных выработках (часть 3)
Задача решается применительно к сыпучей среде, обладающей внутренним трением, но без сцепления.
Рассмотрим на глубине Н выработку шириной 2а (см. рис. 49, д). Над выработкой, согласно гипотезе, образуется свод. Задача сводится к определению формы кривой свода и определению высоты свода.
Для решения первой части задачи рассмотрим условие равновесия дуги ОМ (рис. 50).
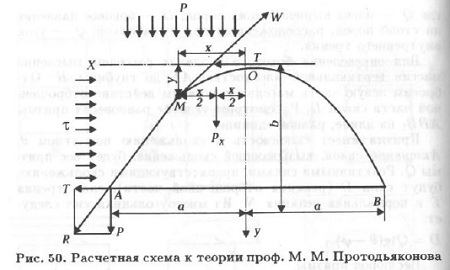
Рассечем свод на две части. Отброшенные части свода ОВ и АМ заменяем действующими в связях силами Т и R. Поскольку часть свода ОМ находится в равновесии, сумма моментов всех сил относительно точки М равна нулю:
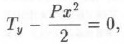
откуда
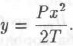
Равенство является уравнением параболы. Так как точка М взята на контуре произвольно, то свод естественного равновесия имеет параболическое очертание.
Для решения второй части задачи рассматривается условие равновесия в пяте свода — точке А. Сила N создает давление на частицы породы и вызывает силу трения, а сила Q стремится сдвинуть опору с места. Для условий равновесия сумма проекций всех сил на любую из осей равна нулю. Спроектируем силы на оси х и у:
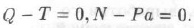
Следовательно, сила трения, возникающая в опоре А:
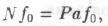
где f0 — коэффициент внутреннего трения.
При сдвигающей силе Q≤Раf0 свод переходит в состояние предельного равновесия.
Для того, чтобы гарантировать его устойчивость, требуется дополнительная величина сопротивления сдвигу. М. М. Протодьяконов ввел величину горизонтального сдвигающего усилия τ. Тогда условие равновесия
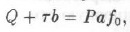
откуда
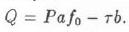
Поскольку Q=Т, уравнение кривой в точке А можно записать в виде
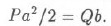
Подставив вместо Q его значение, получим:
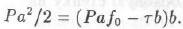
Пo М. М. Протодьяконову, запас устойчивости будет наибольшим, если τ будет иметь максимальное значение. Поэтому, решая уравнение относительно τ и исследуя его на максимум (взяв производную dτ/db), получаем:
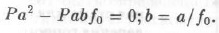
Таким образом, высота свода естественного равновесия равна частному от деления полупролета выработки на коэффициент внутреннего трения. Это основной вывод теории проф. М. М. Протодьяконова.
Окончательно вес пород, оказывающих давление на крепь на протяжении 1 м выработки, имеет вид
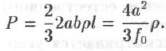
Этот метод расчета горного давления М. М. Протодьяконов распространил и на связные породы, заменив коэффициент трения f0 коэффициентом крепости f. Горное давление не зависит от глубины расположения выработки. Это справедливо для выработок, расположенных на небольшой глубине.
Давление горных пород на крепь выработки со стороны боков определяется по методике, предложенной проф. П. М. Цимбаревичем, исходя из предпосылки образования в стенках выработки так называемых призм сползания. При наличии неустойчивых пород в боках выработки ее стенки разрушаются, опоры перемещаются в глубь толщи горных пород, что увеличивает как размеры свода обрушения, так и давление со стороны боков и кровли выработки.
Величину бокового давления П. М. Цимбаревич предложил определять как активное давление на подпорную стенку от сползающих призм породы m (рис. 51).
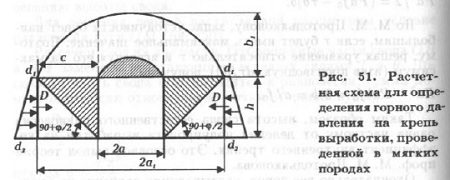
Согласно этой предпосылке крепь в боках выработки работает как подпорная стенка. Давление на подпорную стенку у кровли
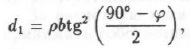
а на уровне почвы выработки
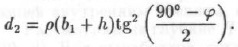
Эпюра давления, действующего на боковую стенку выработки, представляет собой трапецию, и величина горизонтального давления, действующая на единицу длины выработки, численно равна площади трапеции:
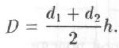
Подставив значения d1 и d2 получим:
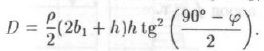
Полупролет свода равновесия
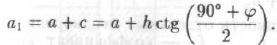
Высота свода
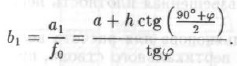
Давление со стороны кровли в случае образования призм сползания запишется формулой
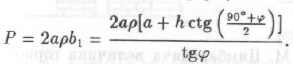
- Расчет горного давления в горизонтальных выработках (часть 2)
- Расчет горного давления в горизонтальных выработках (часть 1)
- Напряженное состояние горных пород вокруг выработок (часть 2)
- Напряженное состояние горных пород вокруг выработок (часть 1)
- Горное давление. Напряженное состояние горных пород
- Расчет параметров проветривания (часть 2)
- Расчет параметров проветривания (часть 1)
- Автотранспорт, конвейеры и безопасность (часть 2)
- Автотранспорт, конвейеры и безопасность (часть 1)
- Грузопотоки и транспортное обеспечение грузоперевозок (часть 3)
- Грузопотоки и транспортное обеспечение грузоперевозок (часть 2)
- Грузопотоки и транспортное обеспечение грузоперевозок (часть 1)
- Выемочно-погрузочные работы в карьере (часть 2)
- Выемочно-погрузочные работы в карьере (часть 1)
- Вскрышные работы
- Подготовка горных пород к выемке
- Вскрытие и подготовка карьерного поля (часть 2)
- Вскрытие и подготовка карьерного поля (часть 1)
- Элементы карьера и технология открытых работ (часть 2)
- Элементы карьера и технология открытых работ (часть 1)
- Компания CATERPILLAR (часть 2)
- Компания CATERPILLAR (часть 1)
- Стадии открытых горных работ при разработке месторождений
- Разработка с поддержанием очистного пространства (часть 4)
- Разработка с поддержанием очистного пространства (часть 3)
- Разработка с поддержанием очистного пространства (часть 2)
- Разработка с поддержанием очистного пространства (часть 1)
- Системы разработки с обрушением руды (часть 3)
- Системы разработки с обрушением руды (часть 2)
- Системы разработки с обрушением руды (часть 1)

