Расчет горного давления в горизонтальных выработках (часть 2)

Первую гипотезу (рис. 49, а) применяют при неустойчивых породах и небольшой глубине заложения выработки (Н≤2а), когда над ней не формируются устойчивая плита или свод естественного равновесия.
Вторую гипотезу (рис. 49, б) применяют в тех же случаях, что и первую, но при глубине Н≥(1÷2)2а.

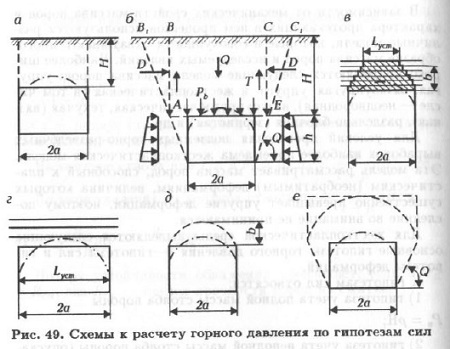
Третья гипотеза предназначена для слоистого массива пород и построена на отыскании предельного пролета Lуст (рис. 49, в, г), при котором слой породы (балка или плита) мощностью m способен сохранять устойчивость. Если Lуст≤2а, то над выработкой может образоваться вывал высотой b, масса которого и определяет вертикальную нагрузку на крепь. Если Lпр≥2а, то кровля выработки устойчива и регулярного давления на крепь выработки не должно возникать.
Четвертая гипотеза предназначена для сыпучих или трещиноватых с небольшим сцеплением пород, способных образовывать над выработкой свод естественного равновесия, воспринимающий на себя давление вышележащей толщи (рис. 49, д, е).
При заложении выработок на небольшой глубине от поверхности столб пород АБСЕ (см. рис. 49, б) под действием собственной массы стремится опуститься в выработку, чему препятствуют силы трения между столбом породы и призмами сползания AВ1В и СС1Е. Горное давление на контакте "массив — горная выработка"

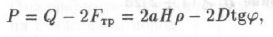
где Q — масса вышележащих пород; D — боковое давление на столб пород, расположенный над выработкой; φ — угол внутреннего трения.
Для определения бокового давления рассечем мысленно массив вертикальной плоскостью АБ до глубины Н. Отбросим левую часть массива и заменим действие отброшенной части силой D. Рассмотрим условие равновесия призмы АВВ1 на длине, равной единице.
Призма имеет склонность к скольжению под углом θ. Активной силой, вызывающей скольжение, будет вес призмы Q. Реактивными силами, препятствующими скольжению, будут сила D (реакция отброшенной части), сила трения Т и нормальная реакция N. Из многоугольника сил следует:

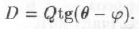
Вес пород призмы

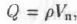
где ρ — плотность пород; Vп — объем призмы единичной площади. Объем призмы Vп =H2tg(90°—θ)/2. Следовательно,

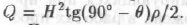
Подставляя значение веса призмы в формулу бокового давления, получаем

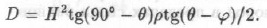
Исследуем функцию на максимум по θ.
Получим

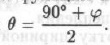
Тогда давление на подпорную стенку

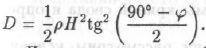
Подставив значения Q и D в формулу горного давления, получим

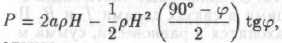
откуда

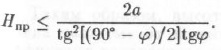
При глубине заложения выработки менее Нпр необходимо пользоваться гипотезой опускающегося столба породы, при глубине более Нпр — гипотезами балок, свода обрушения или другими.
Гипотеза образования над выработкой устойчивого "свода", ограничивающего область деформирующихся при проведении выработки горных пород, изложена в работах проф. М. М. Протодьяконова.

---