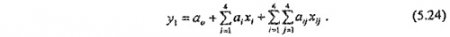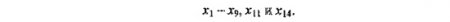Стохастический анализ геотехнологических процессов (часть 2)

Анализ показывает, что небольшая статистическая связь имеется между мощностью залежи и водоприемистостью, а также между водоприемистостью и расстоянием между скважинами.
Тем не менее была сделана попытка построения модели в виде уравнения множественной регрессии по имеющейся информации. Наилучшие результаты относительно у1показало выражение в виде полинома второго порядка

При этом использовались программы с отсевом несущественных факторов. Отсев осуществлялся по двум вариантам. В первом - анализировалась существенность коэффициентов регрессии факторов по критерию Стьюдента, во втором - осуществлялось поочередное добавление факторов по критерию Фишера. В результате обработки информации по первому способу оказалось что из 14 факторов, входящих в модель (5.26), несущественным признан только один - мощность пласта x1. При этом коэффициенты модели есть: а0 = -511,9; а1 = 0; а2 = 117,5; а3 = 13,5; а4 = -10,0; а11 = 0,21; а22 = -4,2; а33 = 1,7; а44 = 0,09; а12 = -2,2; а13 = -0,9; а14 = 0,5; а23 = 1,8; а24 = 0,1; а34 = 1,0.
Средняя ошибка аппроксимации (в процентах) не превышает 1,5%. Коэффициенты множественной корреляции и детерминации близки к единице; средняя квадратическая ошибка оценки по уравнению - менее 0,3 и остаточная дисперсия - менее 0,1. Максимальная абсолютная ошибка аппроксимации составляет менее 4%.
При анализе информации по второму варианту из 14 факторов значимыми признаны:

При этом коэффициенты уравнения регрессии таковы: а0 = -390; а1 =-6,23; а2 = 110,9; а3 = 31,38; а4 =-11,89; а11 = -2,26; а22 = -31,12; а33 = 1,24; а44= 12,57; а12 = -8,88; а13 = 14,92; а14 = 14,92; а34 = -9,9.
Средняя ошибка аппроксимации по этому уравнению не превышает 1,3% при средней квадратической ошибке равной 0,92. Наименьшая абсолютная ошибка менее 6%. Коэффициенты множественной детерминации и корреляции близки к единице, а расчетные значимости уравнения регрессии и коэффициента множественной корреляции значительно превышают табличные значения F и Т критериев.
Отметим, что уменьшение числа факторов резко снижает качество моделей. Так, уже модель, использующая на один фактор меньше предыдущей, дает абсолютное отклонение до 66 % при средней ошибке аппроксимации около 18 %. При этом значимости уравнений регрессии и коэффициента множественной корреляции ниже табличных.
Близкие результаты получены и для других зависимых переменных - извлечения (у2) и добычи со скважины (у3). Удовлетворительные модели получены в виде полиномов второй степени, причем существенную роль играют члены, выраженные через смешанные произведения факторов.