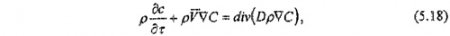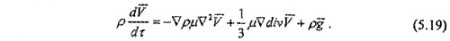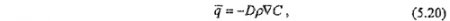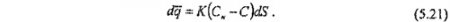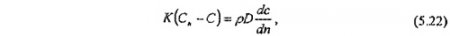Моделирование подземного растворения соли (часть 1)

Практически все геотехнологические методы добычи полезных ископаемых как объекты исследования поддаются изучению с большими трудностями и допущениями. Как уже отмечалось, причина подобного положения заключается в том, что параметры объектов разработки (месторождений) практически недоступны наблюдению и измерению. К тому же горно-геологические и гидрогеологические свойства залежей характеризуются большой изменчивостью. Поэтому затруднено получение информации о свойствах объекта разработки и о закономерностях технологического процесса непосредственно в натурных условиях.
Ввиду этого применение различных методов моделирования наиболее приемлемо для вскрытия общих закономерностей протекания того или иного геотехнологического процесса и определения количественных оценок его технологических параметров.
Использование методов моделирования в геотехнологии можно проиллюстрировать на некоторых примерах.
Процесс растворения соли и закономерности распределения ее концентрации в камере подземного выщелачивания очень сложны. Поэтому при получении математического описания процесса исследователи идут на упрощение физической картины, рассматривая диффузионный и конвективный механизм переноса вещества и гидродинамическое движение вязкой жидкости. Эти явления описываются следующими дифференциальными уравнениями (в изотермическом приближении):
- конвективной диффузии

где D - коэффициент диффузии;
- движения вязкой несжимаемой жидкости (уравнение Навье-Стокса):

Эти уравнения необходимо дополнить условиями на подвижных границах камеры.
Процесс перехода соли с твердой стенки в раствор описывается законом Фика:

где q - количество вещества, перешедшего в раствор с единицы поверхности в единицу времени.
Учитывая, что концентрация рассола в диффузионном слое на границе твердой фазы может быть принята равной концентрации насыщения Сн, количество вещества, перешедшего в раствор с элемента поверхности dS, пропорционально разности концентрации насыщения и растворителя, а также коэффициенту скорости растворения К:

Из уравнений (5.20) и (5.21) получим приближенное уравнение материального баланса на границе камеры:

где n - нормаль к поверхности стенки камеры.
Уравнения (5.18), (5.19) и (5.22) служат основой получения упрощенных математических моделей для процесса подземного растворения, а также для нахождения критериев подобия, обеспечивающих физическое моделирование.

---