Виды моделирования (часть 4)

В основе знакового моделирования лежит исследование явлений с помощью знаковых образований различной природы: схем, графиков, чертежей, формул, графов, математических уравнений, логических соотношений, записанных в символах естественного или искусственных языков. Важнейшей формой знакового моделирования является математическое.
Под математической моделью какого-либо явления обычно понимают систему уравнений (алгебраических, дифференциальных, конечно-разностных и др.) и формул, описывающих протекание изучаемого процесса. Создание математической модели предполагает наличие достаточно полной картины физической природы изучаемого явления. Она может уточняться на основе специально поставленных экспериментов до степени, позволяющей охватить наиболее важные характерные свойства явления. Сущность математической модели состоит в замене исходного объекта его «образом» - математической моделью - и в изучении этой модели с помощью реализуемых на компьютерах вычислительно-логических алгоритмов. Этот метод познания сочетает в себе многие достоинства как теории, так и эксперимента. Работа не с самим объектом (явлением, процессом), а с его моделью дает возможность безопасно, относительно быстро и без существенных затрат исследовать его свойства и поведение в любых мыслимых ситуаций.
В то же время вычислительные (компьютерные, симуляторные, имитационные) эксперименты с математическими моделями объектов позволяют, опираясь на мощь современных вычислительных инструментов информатики подробно и глубоко изучать объекты с полнотой, недоступной чисто теоретическим подходам (преимущество эксперимента).
Неудивительно, что методология математического моделирования бурно развивается, охватывая все сферы от разработки технических систем и управления до анализа сложнейших экономических и социальных явлений.
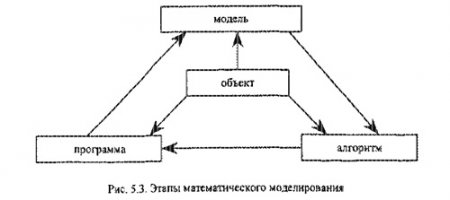
Математическое моделирование условно можно разбить на три этапа: модель-алгоритм-программа (рис. 5.3).

---