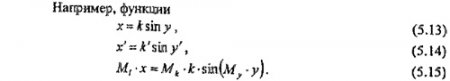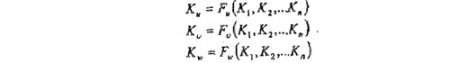Основы теории подобия (часть 3)

Изложенная выше процедура подобного преобразования уравнений справедлива лишь для однородных уравнений. Если подобные процессы описываются уравнениями, содержащими неоднородные функции (трансцендентные, сложные и т.п.), то аргументы этих функций являются критериями подобия.

Чтобы (5.13) и (5.15) были инвариантны, необходимо, чтобы М1/Мk = 1 и Мy = 1, т.е. аргумент, должен принимать одно и то же значение в обоих явлениях т.е. быть критерием подобия.
Вторая теорема. Уравнение связи между переменными, характеризующими явление, может быть составлено из безразмерных комбинаций - критериев подобия. Для всех подобных явлений эти уравнения, называемые уравнениями подобия, численно равны.
Уравнения подобия - это функциональные зависимости определяемых критериев подобия {Ky,Kv, ...,Kw) от определяющих (К1, К2, ..., Кn):

Критерии, составленные из величин, входящих в условия однозначности, называются определяющими. Они выделяют из класса явлений единственное конкретное явление.
Критерии, содержащие зависимую переменную (искомую величину), называются определяемыми.
Уравнения подобия представляют собой конкретные (частные) решения системы основных дифференциальных уравнений, описывающих интересующее нас явление. Конкретная форма уравнений подобия может быть определена двумя путями: эмпирическим и аналитическим.
В другой интерпретации вторая теорема известна под названием π-теоремы: всякое уравнение, связывающее между собой N физических величин, среди которых к обладают независимыми размерностями, а n-неодинаковыми размерностями, может быть преобразовано в уравнение, связывающее N-k безразмерных комплексов и симплексов. При этом число критериев-комплексов равно n-k, число критериев-симплексов N-n. Симплекс - это отношение двух одноименных величин.

---