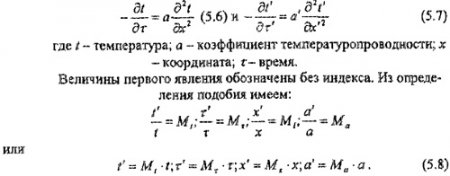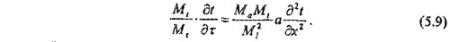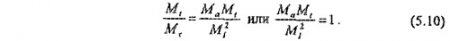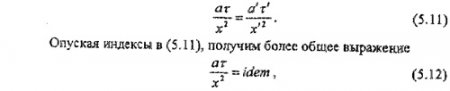Основы теории подобия (часть 2)

Учение о подобии развивалось по двум направлениям: 1) анализ размерностей физических величин, характеризующих явления, 2) анализ уравнений, математически описывающих эти явления.
Первое направление разрабатывалось преимущественно за рубежом, второе - в нашей стране.
Теоремы подобия. Подобие явлений подчиняется некоторым общим закономерностям, которые принято называть теоремами подобия. Эпос теорем три. Первые две устанавливают соотношения между параметрами явлений заведомо подобных. Третья - определяет необходимые и достаточные условия для того, чтобы явления оказались подобными.
Первая теорема. У подобных явлений и процессов критерии подобия имеют одинаковые численные значения, а индикаторы подобия равны между собой.
Критериями подобия называют безразмерные степенные комплексы основных размерных физических величин, входящих в замкнутую систему уравнений и описывающих исследуемый процесс или явление.
Понятие о критериях подобия имеет фундаментальное значение для всех видов моделирования во всех научных дисциплинах. Нахождение критериев подобия представляет одну из важнейших операций в применении теории подобия к моделированию.
Рассмотрим подробнее понятие критерия подобия. Прежде всего это отвлеченное безразмерное число: отношение двух одноименных характеристик процесса. При этом каждая из характеристик может быть составлена из нескольких скалярных или векторных величин. Кроме того, критерий подобия - это не любая безразмерная величина, а та, которая сохраняет числовое равенство для подобных между собой моделей и объекта.
На примере двух подобных между собой явлений, описываемых уравнениями теплопроводности, рассмотрим понятия критериев и индикаторов подобия:

Подставляя значения переменных из уравнения (5.8) в уравнение (5.7), получим

Для соблюдения неизменности уравнений (5.9) и (5.6) необходимо, чтобы

Выражение (5.10) называется индикатором подобия. Подставляя в него отношения сходственных параметров, получим

где idem - означает «одно и то же», т.е. безразмерные комплексы вида ат/х2имеют одно и то же числовое значение для обоих явлений. Выражение (5.12) называется тепловым критерием подобия Фурье.

---