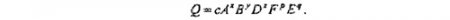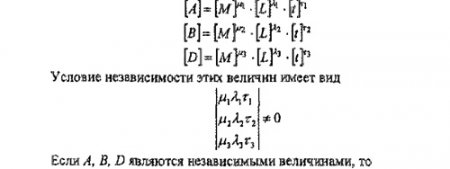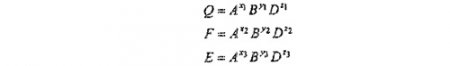Способы вывода критериев подобия (часть 2)

Метод приведения уравнений к безразмерному виду. Для всех переменных величин, входящих в основные уравнения и условия однозначности, выбираются единицы измерения. Затем все переменные величины заменяются их безразмерными значениями, т.е. отношениями к выбранным единицам измерения. Полученные из уравнений степенные комплексы приводятся к безразмерному виду.
При окончательном установлении критериев подобия имеется некоторый произвол, так как критерии подобия можно объединять, перемножать, делить, возводить в любую степень, умножать на числовые коэффициенты и т.д.
Вывод критериев подобия из анализа размерностей величин рекомендуется в тех случаях, когда в связи с большой сложностью и недостаточной изученностью явления система основных дифференциальных уравнений не может быть составлена.
Недостатком метода является возможность неполного учета влияния некоторых важных величин или же, наоборот, включение в число переменных несущественных величин. Поэтому такой анализ сочетается с экспериментом, который подтверждает значимость тех или иных факторов. Большую роль играют также опыт и интуиция исследователя.
Пусть искомая величина Q зависит от величин А, В, D, F, Е. Тогда можно считать, что

Кроме того, известны размерности всех величин. Произвольно выбираются независимые (основные) единицы измерения. Обычно в качестве последних используются масса ([М], кг), длина ([L], м), время ([T] с), температура ([T], ºK), сила тока ([J], а), сила света (кандела), В качестве первичных величин можно выбрать и какие-либо другие единицы измерения. Необходимо только проверить, являются ли они независимыми. Пусть это величины А, В, D с размерностями:


Подставляя вместо А, В и D их размерности, получаем 9 уравнений с 9 неизвестными, которые определяют три критерия подобия.

---