Понятие о горном давлении (часть 1)

Горные породы, расположенные ниже земной поверхности, подвержены действию гравитационных сил. По мере увеличения глубины залегания эти породы испытывают все большие напряжения, но не разрушаются, так как окружающие породы массива также напряжены и противодействуют развитию в какой-либо отдельной его части разрушающих деформаций. Таким образом, общее состояние напряженного массива горных пород — равновесное. Оно изменяется во времени под действием естественных процессов, протекающих в земных недрах. На некоторых участках земной коры эти изменения происходят медленно, за периоды времени, сравнимые с геологическими эпохами, на других, называемых обычно тектонически активными, могут происходить практически мгновенно.
Для получения общего представления о напряженном состоянии массивов и возникающих в них напряжениях допускается рассматривать горные породы как однородные изотропные твердые среды.
Под напряжениями понимается поверхностная плотность внутренних сил; под изотропной средой — горная порода, свойства которой в любом направлении одинаковы. Реальные массивы горных пород представляют собой, как правило, более сложные физические системы. Поэтому для получения численных значений напряжений, возникающих в горных породах, требуется внесение корректив в точные решения математических задач, иногда весьма существенных.
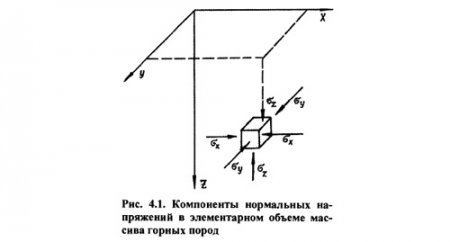
Если в массиве на глубине Н выделить элементарный кубик горной породы (рис. 4.1), то главные напряжения σх, σу, σz, Па, соответствующие по направлению осям координат, можно определить из следующих выражений:


Коэффициент горизонтального распора показывает отношение горизонтальной составляющей напряжений к вертикальной составляющей (σz > σx; σу). Значение коэффициента горизонтального распора определяется для упругих пород через коэффициент Пуассона v из выражения λ = v/(1-v); для сыпучих пород λ = tg2(45-φ/2), где φ — угол внутреннего трения породы, градус. Для идеально упругих пород λ = 0,25÷0,4, для идеально сыпучих λ = 0,27÷0,33.

---