Деформационные свойства при динамическом нагружении

При динамическом нагружении образцов равномерно распределенной по торцу нагрузкой картина нагружения и деформации изменяется по сравнению со статическим. В этом случае в образце возникает волна сжатия, которая будет распространяться вдоль него с определенной скоростью, т. е. в глубь породы деформация распространяется в форме фронта волны. Каждая элементарная частица среды при прохождении фронта смещается на некоторое расстояние, затем совершает несколько затухающих колебаний и успокаивается.
Различают волны продольные, поперечные и поверхностные. Деформации попеременного сжатия и растяжения обусловливают распространение продольных волн. В этом случае направление колебаний частиц среды совпадает с направлением распространения фронта. Продольные волны характерны для всех сред: газов, жидкостей и твердых тел.
Поперечные волны вызываются распространением поперечных деформаций сдвига. Они присущи только твердым телам.
Скорости распространения упругих волн являются упругими характеристиками горных пород и связаны с другими упругими константами. Наибольшей скоростью распространения обладают продольные волны (для большинства пород — 1000...7000 м/с). Скорости продольных ср и поперечных сs, волн связаны с упругими константами пород соотношениями:

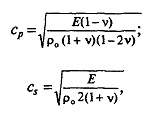
где Е — модуль продольной упругости; v — коэффициент Пуассона; ρo — объемная плотность породы.
Очевидно, что зная скорости распространения волн, можно определить модуль упругости и коэффициент Пуассона. Так как характер и форма деформаций и напряжений в образце зависят от способа приложения нагрузки, полученные значения будут отличаться от тех, которые определены вышеописанными способами. Они получили название динамического модуля упругости и динамического коэффициента Пуассона.
В настоящее время скорость волн чаще всего определяется импульсным методом с помощью ультразвуковой аппаратуры. Сущность метода заключается в определении времени t прохождения импульса от излучателя до приемника по образцу известной длины. В этом случае скорость распространения волн находят по формуле, м/с: ср=l/t, а динамические модуль упругости и коэффициент Пуассона — по формулам

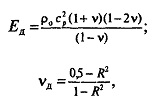
где ρo — объемная плотность, кг/м3; R — отношение скорости поперечных волн к скорости продольных волн.
Еще одной характеристикой упругих свойств пород является акустическая жесткость А, численно равная произведению объемной плотности на скорость продольных волн: А=ρoср. Она характеризует сопротивляемость пород распространению упругих волн, интенсивность затухания волн и определяет характер разрушения пород при взрыве.

---