Деформационные свойства при статистическом нагружении

Модуль упругости горных пород. Для каждого вида напряжений, вызвавших упругую деформацию, существует свой коэффициент пропорциональности между напряжением и деформацией. Этот коэффициент характеризует упругие свойства породы и является ее параметром.
Коэффициент пропорциональности между нормальным напряжением σ и соответствующей ему относительной продольной деформацией εi называется модулем продольной упругости или модулем Юнга Е:

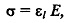
где

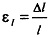
(Δl— абсолютная продольная деформация, l — первоначальная длина образца).
Модуль упругости характеризует жесткость пород, т.е. способность сопротивляться деформации под действием внешних сил.
Модулем сдвига называется коэффициент пропорциональности между напряжением и соответствующей ему деформацией сдвига

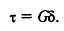
Он характеризует способность материала сопротивляться изменению формы при сохранении его объема.
В отличие от модуля упругости, характеризующего жесткость породы при действии нормальных напряжений, модуль сдвига определяет жесткость породы при действии касательных напряжений. Его численные значения, как правило, меньше значений модуля упругости.
Коэффициент Пуассона устанавливает зависимость между относительными поперечными и продольными деформациями и определяется их отношением:

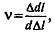
где Δl и Δd — абсолютные продольная и поперечная деформации образца; d и l — соответственно диаметр и длина образца.
Коэффициент Пуассона не превышает значения v=0,5, характерного для несжимаемой жидкости.
При известных значениях модуля упругости Е и модуля сдвига G коэффициент Пуассона может быть определен выражением:

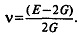
В случае объемного напряженного состояния характеристикой упругих свойств породы является модуль всестороннего сжатия К — коэффициент пропорциональности между действующим напряжением и изменением объема.
Для изотропных тел достаточно знать лишь два упругих параметра, остальные можно вычислить по соотношениям между этими величинами, установленными в теории упругости. Например, модуль всестороннего сжатия:

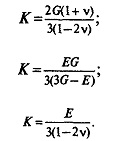
Экспериментально у горных пород чаще других параметров определяют и используют в расчетах модуль упругости и коэффициент Пуассона.
В зависимости от целей использования упругие параметры пород определяют при статическом или динамическом воздействии на них. Модуль упругости большинства горных пород равен 10в3...10в5 МПа. У металлов модуль упругости, как правило, больше, чем у горных пород (Естали=2,2∙10в5 МПа, Емеди=1,2∙10в5 МПа, Еал=7,2∙10в4 МПа).

---