Основные свойства мультифракталов

Массив горных пород, подлежащий разработке, в основном характеризуется двумя важнейшими свойствами - прочностью (крепостью) и ценностями, которые устанавливаются, как правило, путем дискретных испытаний, называемых опробованием. Дискретный характер расположения точек отбора проб на то или иное свойство обусловливает тот факт, что геологическому объекту, как любому природному явлению, при моделировании присуща случайность распределения его показателей в пространстве. Поэтому имеются убедительные основания предполагать, что подобные явления могут быть успешно описаны как случайные фракталы.
Следует определиться, к какому виду фракталов относится вариант установления основных свойств массива. Известны фракталы самоподобия, для которых численно совпадают размерности Хаусдорфа, подобия, поточечная и размерность кластера. Известны фракталы самоаффинные, которые характеризуются локальной и глобальной размерностями и связаны с показателями Херста (H), который еще называется аффинным показателем и может находиться в пределах 0<Нх1. Эта вероятность не зависит от поведения Е(х) при x

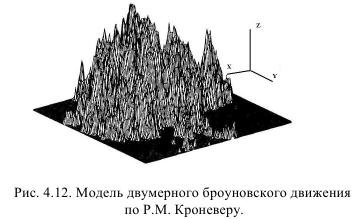
Наша модель поверхности энергоемкости бурения есть двумерный вариант броуновского движения и по аналогии с одномерным (если двигаться по рядам скважин) гауссовский процесс будет двумерным броуновским движением, если он имеет следующие свойства:

и функция Е(х) почти всегда непрерывна.
Случайная величина

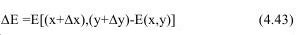
имеет математическое ожидание, равное 0 и дисперсию, определяемую соотношением K2E√Δx2+Δy2 , где К - положительная константа.
Двумерное броуновское движение почти наверняка недифференцируемо, а его фрактальная размерность Д должна быть равна 2,5, так как доказано, что для одномерного движения она равна 1,5.
Условия использования модели, когда вероятность достижения Е(х2) при заданном E(x1) и х<х2 зависит только от x1 и х2, а не от поведения Е(х), побуждают к отысканию процесса, который бы обладал некоторой памятью.
Б. Мандельброт такой процесс назвал фрактальным броуновским движением (ФБД). ФБД удобно определять при помощи показателя Херста, который связан с фрактальной размерностью соотношением:

Поскольку установление D для ФБД весьма проблематично, то проще всего фрактальную размерность можно определить из (4.44):

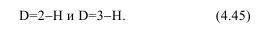
Херст установил, что для многих явлений показатель H находится в пределах: 0<НD0.
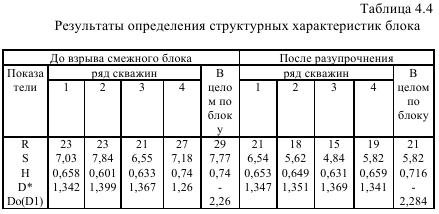
В табл. 4.4 приведены результаты вычислений показателя Херста, локальных и глобальных фрактальных размерностей блока до и после разупрочнения.
При анализе данных табл. 4.4, в частности, показателя Херста и величин размерностей можно заметить, что показатель Херста всегда больше 0,5. При высоких значениях H выясняются достаточно очевидные отклонения статистики энергоемкости бурения от нормального закона Гаусса. В работе Мандельброта рассматривается три случая: H=0,5, Н0,5. При Н≠0,5 имеем случай персистентности или антиперсистентности, т.е. процесс обладает памятью, а при Н0,5 поддерживается имеющаяся тенденция, это означает, что если приращения были положительными в прошлом, то и впредь в среднем будет происходить увеличение E при произвольных а. Для случая Н<0,5 рост в прошлом означает уменьшение в будущем и наоборот.

Эти выводы подкрепляются исследованием процесса (4.40) и (4.41), т.е.

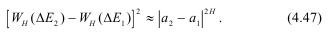
В нашем случае а=6 м, для которого мы получили глобальную фрактальную размерность «поверхности» энергоемкости бурения равную для блока до и после разупрочнения соответственно 2,26 и 2,284, что полностью совпадает с исследованиями, где они установлены для гравитационных волн поверхности моря величиной 2,25 и 2,33.
Определенный интерес вызывает установление связи показателя Херста при его значении, равном 0,5 или близким к нему и расстоянием между скважинами а. Так как H есть функция от а, то подбором а можно определить Н. В нашем случае H=0,5 при а≈16 м, при этом корреляция (4.47) между приращениями и шагом передвижки равна 0, а фрактальная размерность D составит 2,5, что характерно для марковского процесса.
Таким образом, доказано наличие тренда и памяти процесса, что дает основание для правомерного экстраполирования прочностных свойств массива при шаге броуновского движения до 6 -8 м, а также невозможности таких действий при расстояниях более 16 м.
Установлено также, что эффект разупрочнения характеризуется увеличением фрактальной размерности.

---