Оценка фрактальной размерности разрушенного взрывом массива горных пород

Разрушение горных пород, как и других твердых тел, под действием внешнего воздействия начинается с дефекта (назовем его зародышем трещин), который проявляется в виде микротрещин. Под действием нагрузки к одному дефекту присоединяются другие, в результате чего возникает сложная система трещин, а нарастание процесса присоединения приводит к образованию многоуровневой кластер-кластерной структуры, что проявляется в виде трещинообразования.
Уже на этапе возникновения трещин первого уровня формируются частицы разрушенного материала, количество которых затем растет с ростом числа уровней трещин, при этом размеры частиц обусловлены величиной вероятности присоединения трещинных кластеров друг к другу. Чем она выше, тем мельче трещины, и размеры самого кластера растут.
Кластер-кластерная структура по существу означает агрегацию зародышей трещин различной величины. Распределение их в каждом кластере и в общем (конечном) будет подобным, т.е. иметь фрактальное строение и, следовательно, фрактальную размерность Д. Образование систем трещин и дезинтеграция тела на куски разной величины по трещинам в данном случае процессы обратные, но тот и другой процессы - необратимы.
При разрушении породы вероятность роста числа частиц F(x) зависит от поля напряжений, в частности, тензорных полей, обусловленных тензором напряжений:

где σіk - совокупность 9 напряжений, нормальных (i=k) и касательных (i≠k) относительно трех взаимно перпендикулярных площадок; ni - единичный вектор, нормальный к данной площадке.
Вероятность роста Р(σ) будет пропорциональна интенсивности тензорного поля:

Статистическая оценка прочности горных пород, как известно, состоит:

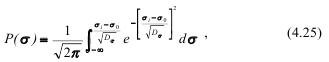
где σi - текущее напряжение; σo - крайняя левая граница прочности; Dσ- дисперсия величины прочности σ.
Оценки следует сравнить:

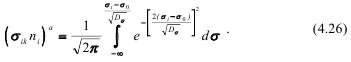
Фрактальная размерность непрерывно изменяется с изменением ‘а’ в уравнениях (4.24, 4.26).
В нелинейной среде потенциально существует спектр структур (форм организации), которые в ней могут появиться под влиянием внешнего воздействия. Этот спектр определяется исключительно внутренними свойствами среды, а не только параметрами внешнего воздействия (σ) и, как теперь известно, еще и временем экспозиции нагрузки. От параметров внешнего воздействия зависят уровни раскрытия трещин или спектр структур, что должно отражаться в изменении фрактальной размерности во времени.
Связь между напряжениями σ и разрушаемым объемом V выражается как:

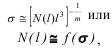
где l - некоторый размер неоднородности; N (l) - число неоднородностей.
Горные породы и массивы, вследствие неоднородности состава и структуры, имеют сложное строение пространства дефектов, дислокаций и других мест «ослаблений», которые представляет собой трехмерную систему условно несвязанных (условно взаимосвязанных) дефектов разной формы и размеров.
Описание структуры пространства дефектов довольно сложная задача, требующая ввода упрощающих моделей и других допущений.
Фрактальный анализ, который можно свести в определению характера изменения фрактальной размерности в процессе разрушения, позволяет перейти к моделям, учитывающим сложность пространственной организации реальной физической системы.
Пусть F(l0) - функция распределения объемов неоднородностей по их характеристическим размерам l0 (характеристический размер - это радиус для сфероподобных дефектов или полуширина для щелевидных). Данная функция входит в состав интегрального уравнения для описания дезинтергации среды и выделение ее из этого уравнения вызывает определенные сложности.
Преобразуем F(l0) к виду:

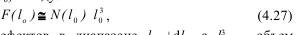
где N(lo) - число дефектов в диапазоне lo+dlo, a l3o - объем занимаемый дефектом размером lo.
Число дефектов N(lo) меняется с изменением их размеров по закону:

для всех lmin В этом случае:

Функция распределения плотности вероятности разрушения среды на объемы при заданных напряжениях выражается как:

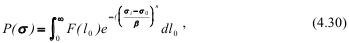
где σi - текущее напряжение; σo - крайняя левая граница прочности; β - параметр подобия или масштабного фактора; n - коэффициент неоднородности.
Подставляя значение F(lo) в (4.30), получим:

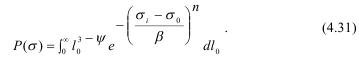
Степенной показатель Ψ является важным параметром, характеризующим фрактальные свойства объекта разрушения. Он связан с фрактальной размерностью Д и выражается как:
Ψ = Д+1.
Зная величину Ψ, можно определить, обладают ли исследуемые системы объемным (при 2<Ψ<3 и тогда 1<Д<3) или поверхностным фракталом (при 3<Ψ< 4 и 2<Д<3).
Для структурированных сред понятие «поверхностный фрактал» означает, что поверхность дефектов является фрактальной, а «объемный фрактал» есть фрактальный объем.
Выражения (4.30, 4.31) могут быть использованы для описания рассеивания энергии разрушения на неоднородностях.
От величины lo зависит вид функции распределения в полном соответствии с величиной раздробленной массы по законам Риттингера, Кирпичева-Кика и Бонда.
Результатом взрывного нагружения массива горных пород является развитие хаотичных структур в виде трещин во взорванном материале. При взрыве зарядов сферической или удлиненной формы только в ближней и средней зоне в пределах 10d3 наблюдается сеть в виде радиальных и тангенциальных трещин, более или менее закономерно распределенная в объеме, за пределами этой зоны проявляется все более хаотичный характер их распределения.
При однократном дроблении массива взрывом для описания гранулометрического состава разрушенной массы возможно использование формулы Розина-Раммлера, например, в дифференциальной форме:

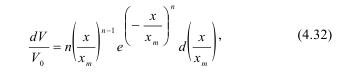
где V/Vo - часть объема, раздробленная на куски больше X по меньше Xm; n - параметр распределения.
Ясно, что отношение V/V0~=x/xm , тогда перейдя от объемов к удельному объему X3 и количеству таких удельных N, составляющих целое тело, имеем:

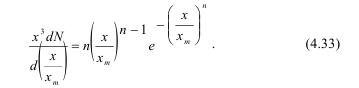
В твердом теле со структурой, где ее роль выполняют отдельности размером Lo и каждая из них имеет неоднородности размером lo, существует равенство:

Если после разрушения произвести рассеивание материала по фракциям, отличающимся своими размерами на Lo, то получим:

Используя закон Розина-Раммлера в виде известной формулы:

ее можно представить в виде графика в координатах lglgl00/R и lgx, а кривая распределения по фракциям обычно представляется прямой с углом наклона к оси lgx:

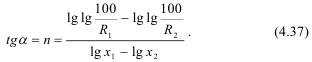
В логарифмических координатах (4.36) 1nР(σ) и ln[(σi-σo)/Р] дает кривую, часть которой представлена прямой, угол наклона ее к оси абсцисс является фрактальной размерностью системы. Вычисление tga по крайним точкам кривой дает усредненное значение такой размерности. Чем круче угол, тем больше размерность, что означает снижение прочности и, следовательно, рациональнее использована энергия взрыва.
Ранее, при оценке результатов взрыва модели, использовалась сетчатая фрактальная размерность по методике М.Ю Яблокова, однако, поскольку изображение плоское, то фрактальную размерность можно также определить по соотношению периметра и площади:

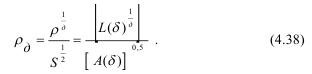
Это соотношением не зависит от размера объекта, но зависит от эталона 5 (размера ячейки сетки) и определяется по зависимости логарифма числа клеток, содержащих границу от числа черных пикселей. Здесь также используется угол наклона участка кривой к оси абсцисс:

A=tgα А=Д-d,

где d=2 - так как имеем плоскость и Д=d-А.

---