Основы физического моделирования разрушения и дробления горных пород

Упругая модель среды. Под разрушением здесь понимается нарушение сплошности материала, конечным итогом которого является дробление материала, характеризуемое разделением на фракции соответствующего гранулометрического состава.
При моделировании обычно пользуются понятием подобия явлений и процессов. Чтобы процесс упругих волновых движений был подобен, нужно принять следующие допущения:
1. Вплоть до разрушения среда ведет себя как упругая.
2. Процесс разрушения происходит мгновенно, интенсивность его определяется лишь величиной напряжений.
Все явления и процессы, происходящие в действительности в реальном времени и при реальных параметрах, относим к натуре, а все те же явления и процессы, но при иных параметрах и за другие промежутки времени - к модели.
При наличии предела прочности материала [σ], то масштаб напряжений равен:

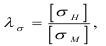
Здесь λσ - масштаб напряжений; σн и σм - соответственно пределы прочности материала натуры и модели.
При соблюдении этого условия на модели число кусков раздробленного материала будет такое же, как и в натуре.
Основные затруднения при реализации этого условия возникают в связи с необходимостью выдерживать соотношения между константами материала модели и натуры, т.е.

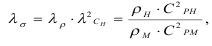
где λσ, λρ, λСр - масштабы напряжений, плотностей и скоростей продольных волн соответственно;
ρн,ρм, Срн, Cрм - плотности материала натуры и модели, скорости продольных волн в материале натуры и модели соответственно.
Это условие выполняется при пропорциональности модулей упругости материалов натуры и модели Eн и Eм для некоторых крепких горных пород это условие выполняется, т.е. можно воспользоваться материалом натуры при создании модели. Однако при этом еще не учтен масштабный эффект. На самом деле процесс разрушения длится конечное время и происходит перераспределение напряжений при трещинообразовании.
При моделировании процесса разрушения, в действительности нужно преодолеть два требования: моделирование задач теории упругости; моделирование задач теории разрушения.
Для первого следует достичь подобия зоны разрушения, т.е. определить ее размеры, или минимальное расстояние от заряда, где материал сохраняет свою сплошность. Для этого достаточно выполнение условия:

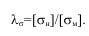
Для второй задачи требуется получить ответ о сохранении или не сохранении структуры материала при заданном нагружении.
Подобие размеров зоны разрушения основано на подобии нагружения упругими волновыми явлениями, т.е. это означает подобие в величинах начальных смещений, или иначе, пропорциональность модулей упругости:

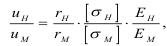
где uн и uм - смещения частиц в натуре и модели;
rн и rм - зоны разрушения в натуре и на модели;
Eн и Eм - модули упругости материала натуры и модели.
Для решения такой задачи имеется критерий подобия Коши:

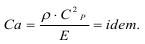
Задачи, связанные с упругими движениями, т.е. скоростью смещений, решаются при соблюдении критерия подобия Эйлера:

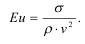
Или иначе:

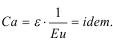
В таком случае необходимо моделировать деформации и напряжения, однако это еще не означает подобия длительности импульса напряжений, ибо он сказывается на интенсивности дробления.
Величина напряжений и длительность импульса зависят от характеристик BB, конструкции заряда и самой среды, где происходит взрыв. К характеристикам BB и среды относятся: скорость детонации, плотность заряжания и акустическая жесткость. Таким образом, для выполнения условий подобия имеется много ограничений, среди них:
- управление длительностью импульса, чаще всего через скорость детонации. При этом возникают новые проблемы, например, с диаметром заряда, верней с критическим диаметром детонации и с количеством продуктов детонации;
- управление напряжениями через импеданс BB и импеданс среды, тогда возникают проблемы с реализацией в модели плотности среды и скорости продольной волны в ней.
Для зарядов одинаковой формы и химического состава их объем и масса пропорциональны l3, так как:

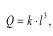
где l - линейный размер; k - удельный вес ВВ.
При сферическом заряде из геометрического подобия следует, что одинаковые напряжения обнаруживаются на поверхности радиусом r, а он пропорционален радиусу заряда ro, т.е.

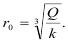
Ho так как r=k1r0, то:

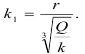
Понятно, что поскольку фигурирует масса заряда, она имеет прямое отношение к количеству выделенной энергии.
Энергетическое подобие является частным случаем термодинамического подобия. Критерий такого подобия включает:
Sэ - этропия системы;
E - энергия системы;
F - свободная энергия системы;
ρ - плотность и удельный объем (V= 1/р)$;
t - текущая координата времени;
T - абсолютная температура.
Термодинамический критерий подобия Наседкина представлен в виде:

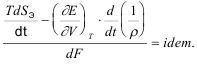
Если плотность среды неизменная, то:

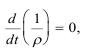
тогда весь критерии можно записать как:

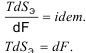
Свободная энергия в поле силы тяжести зависит от высоты подъема породы при взрыве:

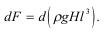
но так как:

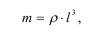
то:

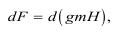
Условие подобия выражается соотношением:

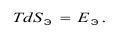
Отсюда критерий подобия соответствует условию:

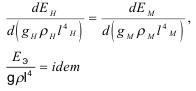
Энергия BB в модели выражается через линейный масштаб:

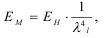
Энергия заряда в модели меньше в 4-ой степени от геометрического масштаба самой модели, а масса меньше в 3-ей степени:

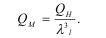
Возможность моделирования по энергетическому критерию или по критериям Эйлера, Коши и Фруда предусматривает соблюдение масштабов:
- плотности,
- гравитационного поля,
- напряжений и модулей упругости и др.
Только в этом случае можно соблюсти геометрическое, кинематическое и динамическое подобие систем. Соблюдение всех названных условий практически невозможно, особенно это касается процессов разрушения горных пород и массивов, когда нельзя избежать влияния масштабного эффекта. Одним из способов решения задач замены природного (натурного) материала в модели является моделирование на так называемых эквивалентных материалах. Их свойства находятся в определенных соотношениях со свойствами материала натуры.
Из уравнения механического подобия Ньютона можно получить такие условия подобия:

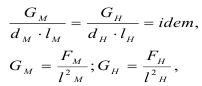
где Gм, Gн - любая механическая характеристика модели и натуры (модуль упругости, предел прочности и т.п.);
Fм, Fн - силы, действующие в модели и в натуре;
lм, lн - линейный размер модели и натуры;
dм, dн - удельный вес материалов модели и натуры.
По этим условиям можно получить деформации горных пород в сходственных точках натуры и модели. Такие условия являются частным случаем критериев подобия для упругой среды, когда действующие силы определяются весом породы:

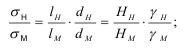
где Нн, Hм - любые линейные размеры;
γн, γм - размерность плотности, удельного веса, объемного веса. Так как размерность напряжений σ=F/l2, то:

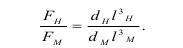
Если Gн и Gм - это любые механические характеристики, то:

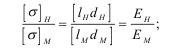
При γ=ρg, получим:

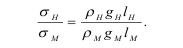
Каждое из этих отношений является соответственно масштабами напряжений, плотности, сил тяжести и линейным масштабом, что можно выразить как:

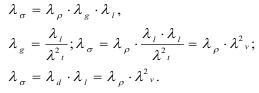
Профессору В.Р. Именитову принадлежит идея применения эквивалентных материалов для моделирования динамических задач. Метод основан на предположении, что подобные куски горной породы должны подобным образом размещаться в обрушаемом массиве при соблюдении условий подобия действующих сил. Основным условием получения подобного расположения является дробление материала модели и натуры на геометрически подобные куски. Распределение кусков породы в развале подчиняется силам тяжести.
Выполнить все условия подобия в таком случае невозможно, например, - прочностное подобие. Поэтому создается модель среды из геометрически подобных кусков прочного материала, скрепленных слабым цементом. Под действием взрыва такой материал разрушается по местам соединения кусков, т.е. искусственно создается столько же центров трещиноватости, что и в натуре.
Подобие взрывного нагружения устанавливается из подобия развалов в натуре и модели, а именно его параметров:
- ширины и высоты развала;
- формы и коэффициента разрыхления.
Подобие этих параметров зависит от скорости смещения частей массива, т.е.

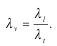
При этом величина зарядов BB на модели определяется из условия подобия векторной картины:

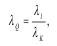
где λк - масштаб влияния работоспособности BB, объемного веса и прочности среды.
Масштаб диаметра заряда определится как:

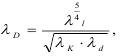
где λd - масштаб объемного веса.
Метод эквивалентных материалов успешно применяется при моделировании воронки выброса, разлета породы и в других случаях. Реализация метода затруднена, если соблюдать условие:

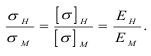
Ho если использовать другое условие в виде:

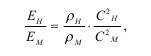
где Сн, Cм - скорости волны напряжений в материале натуры и модели, то трудности устраняются.
Метод эквивалентных материалов может быть использован при исследовании различных методов управления действием взрыва при дроблении горных пород, при этом гранулометрический состав раздробленной массы задается.
Основными методами управления энергией взрыва являются:
- изменение конструкции заряда,
- регулирование сетки скважин,
- подбор типа BB,
- выбор диаметра заряда,
- подбор плотности заряжания и др.
Дробление пород зависит от этих условий. Менять все условия в натуре достаточно сложно и трудоемко.

---