Формирование поля напряжений при взрыве сосредоточенного и удлиненного зарядов

Поле напряжений при взрыве заряда BB в горной породе формируется за счет переданного ей импульса, величина которого у сосредоточенного и удлиненного зарядов разная. Рассчитаем его величину, для чего воспользуемся рекомендациями О.Е. Власова.
Предварительным условием к расчетным схемам являются следующие предположения:
- детонация происходит мгновенно, чего в действительности не бывает;
- отсутствует сопротивление окружающей среды, что также нереально.

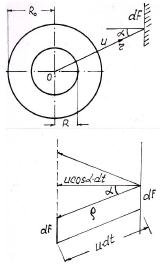
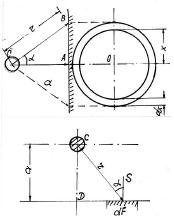
Примем следующую расчетную схему (рис. 3.7). В силу симметрии взрывные газы (продукты взрыва) разлетаются равномерно во все стороны со скоростью u и она будет совпадать по направлению с радиусом r. Если радиус заряда R0, а r расстояние до элемента dF, то любая частица внутри заряда на расстоянии R от центра будет двигаться по окончании детонации. Через время t1 частица переместится на расстояние Ro-R со скоростью w, тогда для этого потребуется время:

Дальше эта частица будет двигаться со скоростью и до встречи с преградой и пройдет путь r-R0, время ее движения равно:

Общее время, когда частица ударит о преграду dF, составит:

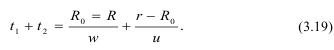
Ho так как Ro>R>0, то время, в течение которого преграда находится под действием продуктов взрыва, составит:

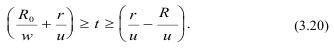
Из (3.20) продолжительность действия продуктов взрыва на преграду определится как:

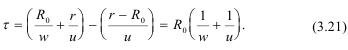
Будем различать плотности покоящихся газов (т.е. самого заряда BB) ρ0 и движущихся продуктов детонации ρ1.
Смещение поверхности разлета за время dt равно wdt, сами частицы на поверхности заряда за это время пройдут расстояние udt. Газы, занимавшие объем wdt через dt заполнят объем (w+u)dt, имея в виду, что они давят на площадку dF. Так как масса газов не изменяется, то:

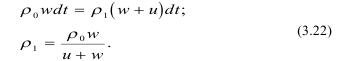
При движении объем продуктов детонации будет увеличиваться пропорционально увеличению поверхности сферы, тогда вблизи преграды плотность продуктов детонации определится как:

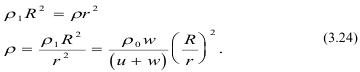
При подходе к преграде dF имеет место удар частиц подобно идеально упругим шарам, а нормальная скорость меняет знак на обратный.
Импульс dS, действующий на преграду при массе газов ρucosα dFdt=m (dV=udtdF).
В соответствии с законом Ньютона, изменение импульса составит:

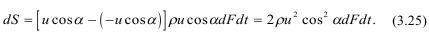
Подставляя (3.24) в (3.25), имеем:

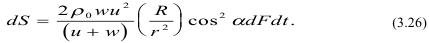
Давление на преграду найдем, разделив обе части на dFdt:

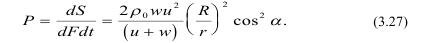
Для определения P нужно знать как давление изменяется во времени t. Его можно определить, продифференцировав (3.19):

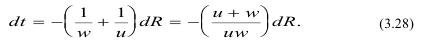
Имея в виду (3.27) и (3.28), получим значение импульса:

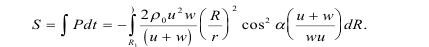
Пределы изменения R указаны в соответствии с изменением t так как начало движения соответствует R0=R, а конец при R=0. Интегрирование дает:

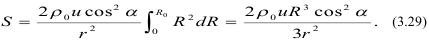
Масса заряда С связана с R0:

тогда импульс составит:

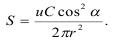
Обозначим u/2π=А, тогда величина импульса окажется равной:

Полный импульс от взрыва сосредоточенного заряда, действующего на неограниченную плоскость на расстоянии а от центра заряда определится, если вырежем кольцо в плоскости радиусом X и шириной dx (рис. 3.5).
Площадь кольца равна:

Удельный импульс, приложенный к единице поверхности кольца определяется из (3.31). Из треугольника ABC имеем:

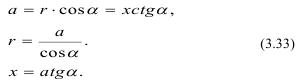
Подставляя эти значения в (3.30), получим:

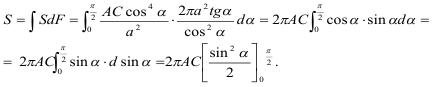
Полный импульс составит:

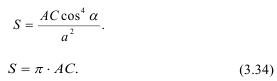
Для цилиндрического заряда большой длины, когда разлетом в торцах можно пренебречь, действие на неподвижную преграду выражается теми же формулами. Уравнения (3.19) - время удара частиц, (3.21) - продолжительность т действия, (3.22) - плотности движущихся продуктов детонации остаются в силе вследствие осевой симметрии.
Увеличение же боковой поверхности цилиндра будет пропорционально первой степени от радиуса, и плотность продуктов взрыва р (3.24) выразится как:

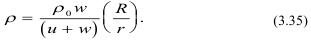
Давление на элементарную площадку (рис. 3.8), как и ранее, определим как:

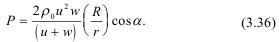
Интеграл по времени t дает значение удельного импульса:


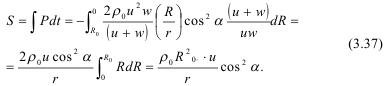
Если длина заряда L, то его масса С равна:

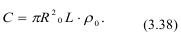
Тогда импульс равен:

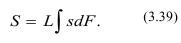
Если преграда находится на расстоянии а, то полный импульс равен:

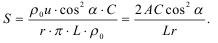
Элемент поверхности составляет:

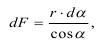
тогда импульс определится как:

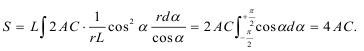
Сравнивая величины полного импульса от сферического и цилиндрического зарядов, становится ясно, что они соотносятся как π/4, т.е. импульс от сферического примерно на 30% меньше, чем от цилиндрического.

---