Формирование поля напряжений и энергозатрат при разрушении горных пород взрывом

Представление о механизме разрушения горных пород взрывным нагружением дополняется новыми экспериментальными результатами. В данном случае опыты были поставлены на органическом стекле толщиной 5 мм со следующими физико-механическими свойствами: плотность ρ=1,19 г/см3, скорость продольной волны Cp=2,14 км/с, модуль Юнга Е=550 МПа, коэффициент Пуассона μ=0,358, предел прочности на растяжение [σр]=55МПа, предел прочности на сжатие [σсж]=85 МПа.
Пластине из оргстекла придавали форму уступа (рис. 4.1) высотой 20 см с углом откоса 64°. Размеры модели выбраны таким образом, чтобы исключить влияние торцов и боковых поверхностей на процесс развития волновой картины, при этом геометрический масштаб с учетом подобия волновых движений оказался равным 1:138. Заряд BB представлял собой бумажный патрон с ТЭНом массой 0,2 г плотностью от 0,8 до 1,26 г/см3 и скоростью детонации D= 6700-7200 м/с. Высота столба заряда составляла 6,5 см и диаметр 1,8 мм.

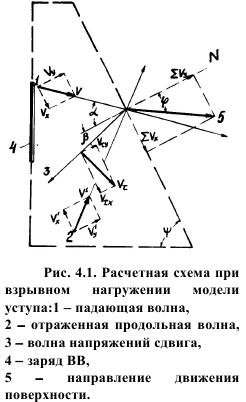
Имея ввиду развитие волновой картины и полей напряжений под воздействием взрывных нагрузок (рис. 4.1), на плоскость откоса в разных его местах по высоте уступа помещали кусочки оргстекла из той же пластины размерами 5*5*15 мм массой 0,446 г, находящихся на различных относительных расстояниях от оси заряда. На поверхности откоса кусочки располагались свободно, имитируя трещину, или приклеивались в тех же точках специальным клеем, способным передавать скалывающие напряжения, а для контакта использовалась обычная вода.
Процесс взрыва фиксировали двумя скоростными кинокамерами синхронно работающими в режиме лупы времени с частотой кадров в секунду соответственно СФР - 187000 и CKC-1м - 3100. Сверхскоростная камера СФР-1 служила для фиксирования начальных скоростей, а камера CKC - текущей скорости.
По фотоотпечаткам с обеих камер рассчитывали скорости полетов кусочков, окрашенных в черный цвет, которые хорошо различимы на белом фоне построением кинограмм.
Управление углами падения волн напряжений и, следовательно, углами отраженных волн и направлениями движения свободной поверхности, в эксперименте реализовывалось при прямом и обратном инициировании удлиненных зарядов, а также изменением плотности заряда ТЭНа, от которой зависит скорость детонации в соответствии с зависимостью:

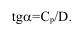
Угол траектории полета связан с углом откоса ψ соотношением:

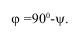
Для упругого тела соотношение между φ и α связано с коэффициентом Пуассона, который в данном эксперименте являлся критерием согласия:

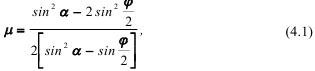
где α - угол падения фронта волны напряжений на поверхность откоса;
φ - угол между направлением полета и нормалью к поверхности откоса.
Критерий согласия позволял судить о правильности результатов в случае с приклеенными кусочками, сущность согласия состояла в следующем. В случае свободно лежащих кусочков на плоскости откоса они должны двигаться по направлению перпендикулярному к плоскости, а при приклеенных - по некоторому направлению, обусловленному волной сдвига, и тогда при упругом поведении величина коэффициента Пуассона должна составить μ=0,327-0,387. Ho в связи с тем, что кусочки приклеены клеем, снижающим упругие свойства, реальная величина коэффициента должна приближаться к 0,400. Результаты экспериментов представлены в табл. 3.2, часть 3 и на рис. 4.2.

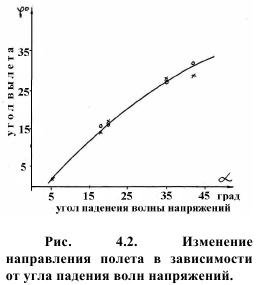
В среднем по эксперименту коэффициент Пуассона оказался равным 0,410. Возможные погрешности в определении начальных направлений полета или скорости детонации обусловили появление расчетных μ несколько больших предельных значений, однако в среднем величина их не превышала 0,360-0,410, что подтверждает выдвинутые гипотезы о механизме взрывного воздействия на модель массива.
Как следует из табл. 3.2, верхняя треть уступа как при прямом, так и при обратном инициировании движется под одинаковыми углами, что связано с возникновением полусферы верхнего торца (аналогично и нижнего) заряда. Остальные 2/3 уступа в зависимости от направления инициирования движутся под различными углами.
Для условий эксперимента угол вылета пилот-куска определялся зависимостью:

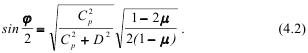
Соотношение показывает, что направление движения свободной поверхности изменяется в зависимости от свойств среды и детонационных характеристик ВВ. Чем выше скорость детонации D, тем меньше угол φ и тем ближе вектор скорости к нормали N, а сама скорость больше по величине. Аналогичное влияние оказывает коэффициент Пуассона на направление полета и величину скорости.
Величина средней начальной скорости полета изменяется в зависимости от относительного расстояния r=R/d (d - диаметр заряда) по закону:

и конкретно для открытого и закрытого заряда данного эксперимента:

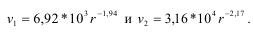
В случае закрытого заряда, за счет поддержания давления продуктов взрыва (ПВ) в зарядной камере более длительное время, скорости возрастают по величине почти в два раза и, соответственно поддерживается более высокий уровень энергии волн напряжений.
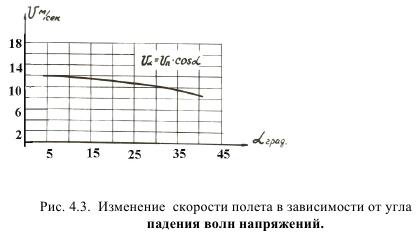
Эксперименты показали также, что различие в углах падения волны напряжений отражается на величине скорости полета (рис. 4.3):

Вместе с тем, установлено, что степень изменения скорости, обусловленная ростом относительного расстояния, выше, чем под влиянием угла падения волны сжатия. Поскольку угол падения зависит от скорости детонации с одной стороны и упругих свойств среды, - с другой, то:


Тогда и скорости полета соответственно можно выразить, используя детонационные характеристики BB и упругие свойства среды:

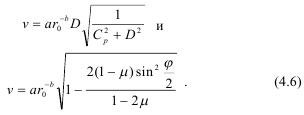
Качественный анализ уравнений (4.6) показывает, что при увеличении скорости детонации, увеличиваются и скорости полета, при прочих равных условиях.
Повышение скорости деформации путем увеличения скорости нагружения (D) означает локализацию зоны пластических деформаций и перевод оставшегося объема среды в группу хрупкого разрушения, особенно это касается отраженной волны, что, несомненно, приводит к увеличению скорости полета. Этим анализом установлено, что уменьшение коэффициента Пуассона, как правило, приводит к меньшему углу отклонения вектора скорости от нормали, т.е. к росту скорости. С другой стороны, уменьшение μ свидетельствует об уменьшении доли вязкого разрушения и, следовательно, меньшим энергозатратам, свойственным хрупкому разрушению.
Повышение скорости нагружения среды позволяет снизить прочностные ее свойства и вместе с этим и энергетические затраты, а также приводит к переходу от вязкого разрушения путем среза к менее энергоемкому процессу разрушения посредством отрыва, что следует из соотношения между максимальными касательными и растягивающими напряжениями в соответствии с объединенной теорией Давыденкова-Фридмана.
Скоростная картина определяет уровень напряжений под действием взрывной волны, который можно установить по известному из теории упругости соотношению:

где u - массовая скорость смещения частиц за фронтом волны, обычно она равна половине скорости полета v, т.е. u=v/2.
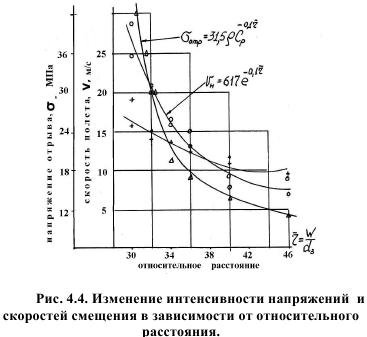
С учетом этих соотношений, напряжения в зависимости от упругих характеристик среды и детонационных параметров BB, включая и энергетические, выразятся как (рис. 4.4):

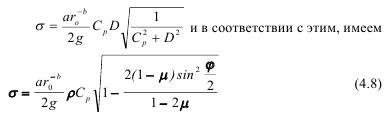
Имея в виду то, что скорость детонации зависит от теплоты взрыва, т.е. от потенциальной энергии BB (Qv), получим (4.9):

где n - показатель политропы, для BB плотностью рвв>1, принимается равным 3.
Напряжения определяются как:

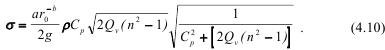
Эти уравнения показывают пути управления уровнем напряжений, которые растут в падающей и соответственно в отраженной волне при увеличении скорости нагружения массива.

Обратим внимание на составляющую часть всех приведенных соотношений - акустическую жесткость среды рСр Из (4.7) следует, что:

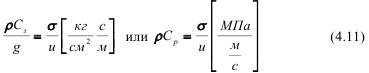
Акустическая жесткость численно соответствует напряжению, созданному ударом по породе со скоростью 1 м/с. Зная табличные данные нашей модели, так называемое удельное давление составит 2,52 МПа/м/с. Следует предположить, что это является некоторой константой среды. Очевидно, что можно определить критическую скорость разрушения, соответствующую временному сопротивлению отрыву и сжатию для оргстекла, которые соответственно равны: [σотр]=55-60 МПа и [σсж]=80-90 МПа. В этом случае имеем:

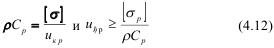
Вычисленная критическая массовая скорость смещения за фронтом волны составит соответственно Uкр (от) = 22-24 м/с и Uкр (сж) = 32-36 м/с.
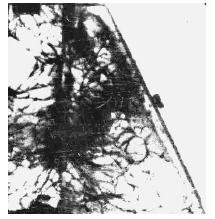
Фактически максимальная величина скорости полета составила 44,5 м/с, т.е. вполне соответствует критической скорости разрушения при отрыве, средняя же скорость смещения поверхности откоса составила 32,6 м/с. Именно поэтому модель не разрушилась, а покрылась трещинами с далеко неодинаковой плотностью (рис. 4.5).

Определим величину энергии отраженной волны в данном эксперименте, которая согласно законам акустики составляет:

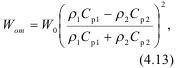
где ρ1, ρ2 и Cp1, Cp2 - плотности и скорости продольных волн во взрываемой среде и на плоскости откоса уступа.
Поскольку ρ2—>0, то Wот =W0, т.е. интенсивность отражения волны почти равна интенсивности падающей волны в каждой точке пространства. Вместе с тем, энергия падающей волны затухает по закону 1/r3 или 1/r2. Энергия отраженной волны реализуется в виде смещения плоскости откоса и ее доля в виде энергии движения куска оргстекла составляет:

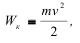
где V - скорость движения условной плоскости откоса уступа, м/с; m =0,446; г - масса куска.
При площади кусочка оргстекла ΔS=0,075 см2, энергия, приходящаяся на единицу площади составит 0,31 МДж/м2, а на всю плоскость откоса 11см2 - 0,341 КДж. Потенциальная энергия заряда BB из ТЭНа в 0,2 г при плотности рвв =1,26 г/см3 соответствует 1,1 КДж. Учитывая, что закон затухания интенсивности напряжений аналогичен изменению массовой скорости смещения за фронтом волны, величина энергии отраженной волны растяжения на плоскости раздела сред окажется равной:

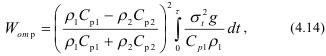
где т - время пробега волны от свободной поверхности к зарядной камере, которое для условий эксперимента равно 52 μс.
Оценка величины энергии отраженной волны показывает, что они составляет около 0,65 КДж или 6% от потенциальной энергии ВВ.
Представляет интерес и оценка энергии разрушения модели. Известно, что разрушающим напряжением является такое, которое включает в себя составляющие сопротивлению растяжению и сдвигу, в полном соответствии с волновой картиной. Имея ввиду, что тсдв>σраст, удельная работа разрушения связана с критической скоростью разрушения:

Эта же удельная работа зависит от разрушающего напряжения σраз, упругих E и пластических показателей Кпл:

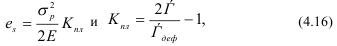
где Кпл - коэффициент пластичности; Едеф. - модуль полной деформации, обычно Едеф<Е.
Имеется более простая оценка Кпл через:

Приравнивая (4.15) и (4.17), получим:

Модуль полной деформации определяется из (4.18):

По нашим оценкам при известном uкр = 22 м/с, Едеф = 96,5 МПа, в этом случае коэффициент пластичности составит К'пл =5,7. Удельная работа разрушения окажется равной:

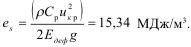
Потенциальная энергия заряда составляет всего 1,1 КДж, при взрываемом объеме 100 см3, запаса этой энергии недостаточно для полного разрушения модели и разброса кусков, что отчетливо видно по результатам, когда модель неравномерно покрывается трещинами, а нижняя часть уступа оказывается ими слабо покрыта.
Результаты экспериментальных исследований данного этапа подтвердили, что механизм разрушения горных пород взрывом формируется за счет возникновения сложной векторной картины скоростей смещений элементов уступа, обусловливающей соответствующие сдвиговые и растягивающие напряжения и энергетически предпочтительные затраты.
Интенсивность разрушения модели может быть рассчитана, если предположить, что она имела дефекты размером l0, которые при взрывном нагружении срастаются в системы взаимно пересекающихся трещин и образуют отдельности размером L0.
По многочисленным (более 50) нашим экспериментам на пластинах из оргстекла, имитирующих откос уступа, можно установить параметры неоднородности модели, следуя методологии В.Н. Родионова.
Фотоотпечатки процесса детонации модельного скважинного заряда и разрушения всей модели позволили установить время разрушения, которое составило 320*10в-6 с. Зная длину заряда lз равную 6,5 см и скорость детонации ТЭНа плотностью 1,26 г/см3 -7200 м/с, установим продолжительность положительной фазы волны сжатия, характеризующей скорость деформации, которая в свою очередь определяет период времени до разрушения:

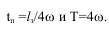
Расчеты показали, что tп составило 0,225*10в-5 с и период колебаний Т=0,9*10в-5 с, соответствующий частоте f=0,l1 МГц.
Время до разрушения модели определяется величиной деформации и временем полупериода нарастания давления до максимума и разрядке, т.е. переходу к отрицательной фазе:

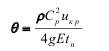
В нашем эксперименте Q равно 2,45*10в4 с.
Минимальный размер неоднородности зависит, как известно, от добротности материала, являющемуся по В.В. Ржевскому обратной величиной логарифмического декремента затухания:

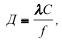
где λ - коэффициент поглощения, имеющий размерность 1/м, и для горных пород колеблющийся от 0,05 до 0,5; С - скорость волны, м/с; f - частота колебаний, МГц.
Коэффициент поглощения в работе П.С. Миронова определяется по эмпирической формуле:

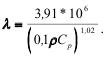
При анализе имеющегося экспериментального материала других авторов установлено, что показатель поглощения для продольных λp и поперечных λs, волн одной и той же породы отличается существенно, как правило, на 30-50%. Простейший ранговый корреляционный анализ свидетельствует, что не существует связи между показателем поглощения продольной волны и коэффициентом Пуассона, в то время как таковая связь установлена для показателя поглощения поперечной волны и коэффициентом Пуассона с коэффициентом корреляции 0,66. Вероятно, это объясняется преобладанием поперечных деформаций при нагружении в волне сдвига. По этой причине с большой вероятностью можно утверждать, что величина коэффициента поглощения численно близка к коэффициенту Пуассона для данного материала, т.е. в нашем случае λ=0,380.
Поскольку добротность Qм равна:

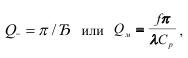
для нашего случая она составляет 2,26*10в3, что вполне соответствует, например, добротности канифоли, принятой равной 10в3.
Минимальный размер неоднородности l0 связан со скоростью релаксации vp/l0=vp*Q и оказался равным 4,9*10в4 м. Скорость релаксации для стекла и других относительно бездефектных материалов принята 2*10в-8 м/с.
Размер неоднородности l0 можно установить по известным разрушающему напряжению σраз и акустической жесткости среды, а также по известному соотношению скорости релаксации и скорости деформации:

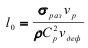
В нашем случае σраз составило 56 МПа, a Vр=2*10в-8 м/с и Vдеф =4,68*10в-6 1/с. Размер неоднородности окажется равным 4,48*10в-4 м, т.е. достаточно близко к установленному выше.
Выполненные расчеты размеров неоднородностей и разрушенных отдельностей позволяют сопоставить их со средним числом кусков nср на поверхности откоса, рассеченного трещинами. По нашим подсчетам nср колеблется в пределах 22-29 штук, при длине откоса 220 мм средняя отдельность составляет 8,5-10 мм, что довольно близко к найденной выше величине.
Конструкция модели в целом и образование зарядной камеры позволила установить процесс развития деформации изгиба во времени. Зная действительные размеры всех элементов модели, измерениями величины прогиба по линии, проходящей через середину заряда, вычисляли максимальную величину прогиба f, а также определяли ударную вязкость материала ау = А/F, где А - работа удара, F - площадь сечения пластины Б (рис. 4.6).

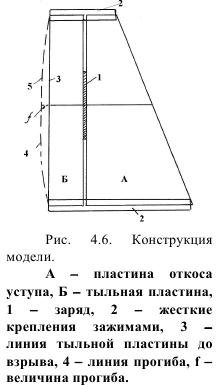
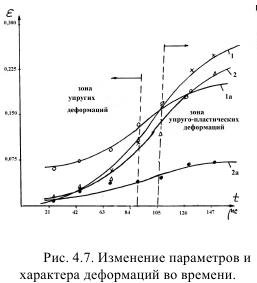
Для анализа и измерений были произвольно выбраны по два эксперимента с прямым и обратным инициированием. Результаты сведены в табл. 4.1, по данным которых построен график рис. 4.7.

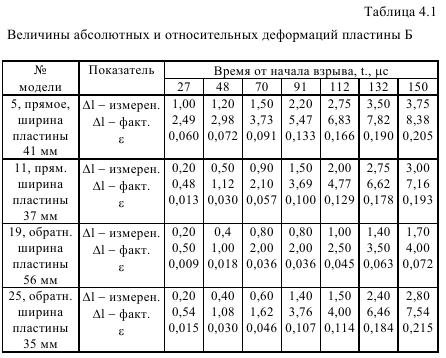
Анализ графиков показал следующее.
1. Прослеживается явный прогиб кривых, ограничивающих область упругих деформаций и переход в область упругопластических, причем, как правило, он отмечается в районе 90 μс от начала взрыва, что абсолютно соответствует перегибу на графике измерения фрактальной размерности во времени.
2. Все кривые имеют в начале процесса короткий участок «разгона» деформации до 50μс от начала взрыва, затем участок довольно хорошо согласующийся с законом Гука (до 90 μс) и далее участок упруго-пластического течения и, начиная со 105 μс явное разрушение тыльной пластины.
3. Развитие деформационного процесса при прямом инициировании в области упругих деформаций выше, чем при обратном в среднем на 30%, в то время как в области упругопластических деформаций выше всего на 10%.
Результаты экспериментов позволили также определить величину ударной вязкости пластины из оргстекла, которая при площади сечения 1,75 см2 и работе удара в 1,1 КДж, оказалась равной 0,63 КДж/см2, что вполне укладывается в известные пределы.

---