Основные закономерности процесса разрушения горных пород взрывом

В.Н. Мосинец утверждает, что параметры генерального разрушения твердых сред определяются в основном законами волнового движения, т.е. параметрами волн сжатия и растяжения, а также условиями рассеивания энергии в неупруго-деформируемых средах с увеличением расстояния от источника возмущения до точки исследования.
Взрыв BB в твердой среде вызывает ударную волну сжатия вблизи заряда за счет скачка давления газообразных продуктов, порода переходит в текучее состояние (измельчается), так как давление во фронте волны во много раз превышает временное сопротивление сжатию (σсж). С расстоянием поток энергии ослабевает и волны сжатия способны образовать трещины в местах, где скопились дефекты различных размеров, а давление во фронте волны только немного превосходит (σсж), однако трещины могут продолжить развиваться за счет концентрации напряжений на их концах, теперь уже в виде растягивающих напряжений (σpac), которые существенно ниже (σсж).
Наконец, в наиболее удаленных от центра взрыва точках, где давление существенно меньше, чем (σсж) наблюдаются упругие колебания среды без заметных нарушений, что называется зоной рассеивания энергии.
При наличии свободной поверхности волна сжатия, достигая ее, отражается от среды с иной акустической жесткостью по законам акустики, превращается в волну растяжения. Энергетические соотношения между двумя волнами могут быть описаны на основе учета разности в акустической жесткости двух сред:

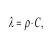
где ρ - плотность среды; С - скорость звука в среде.
Чем больше различаются между собой эти две среды, тем меньше энергии проходит во вторую среду, т.е. большая ее часть сохраняется в отраженной волне.
Если отношение акустических жесткостей сред обозначить т, то количество отраженной энергии и прошедшей во вторую среду будут соответственно равны:

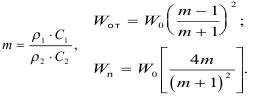
где W0 - энергия падающей волны.
Эти соотношения показывают, что определение количественных закономерностей процесса разрушения горных пород взрывом может быть произведено на основе изучения движения волн напряжений и известных законов сохранения материи (массы, количества движения, энергии).
Ударная волна и волна напряжений имеют одно и то же происхождение. Однако ударная волна присуща для идеальных газов (жидкостей), где сила тяжести, вязкость и модуль упругости постоянны. В горных породах этого не наблюдается и, следовательно, условия прохождения волна не стабильны. Значит, структурный характер волна иной, но качественная картина тих волн единая. Для ударной волны характерна скорость распространения выше скорости звука в данной среде или ее скорость выше, чем скорость деформации среды.
Законы волнового движения. Огромное давление, приложенное к стенкам зарядной камеры, передается к другим точкам среды в виде волнового параметрами. движения, скорость которого выше скорости звука в этой среде. Распространение волна вызывает местные подвижки- смещения среды с изменением ее внутреннего напряженного состояния. В зависимости от крутизны фронта (угол φ) и закона затухания, различают две формы разрыва, т.е. изменение давления во фронте волны (рис. 3.15):
а) волна сжатия с крутым передним фронтом и экспоненциальным затуханием заднего фронта - оба показателя по форме похожи на ударную волну;
б) волна сжатия, передний фронт которой связан с определенным временем нарастания и изменяется примерно так же как фронт затухания, - она представляет волну нагрузки.

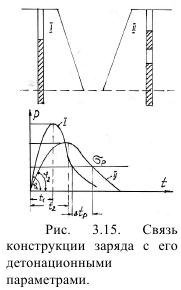
Обе волны - это результат скачка изменения состояния среды, которое определяется законами сохранения массы, количества движения и энергии.
Закон сохранения массы. На элементарном объеме среды dv=dxdydz, в результате изменения плотности среды ρ0 в процессе сжатия до состояния ρ, в точке x, y, z за время dt изменение массы представляется как:

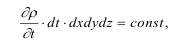
такое возможно в случае изотропии свойств среды.

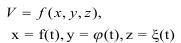
В действительности горная порода анизотропна, т.е. по осям x, y, z изменение объема неравномерное, а также неравномерно оно изменяется и во времени. Тогда:

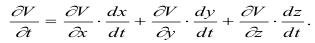
Подставляя последнее уравнение в исходное, получим:

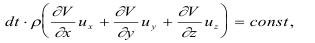
где ux, uy, uz - скорости деформации элементарного объема dV по осям x, y, z.
Закон сохранения количества движения. В соответствии со вторым законом Ньютона имеем выражение импульса через силу F и время t воздействия ее на элементарный объем dV:

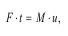
где M - масса среды, вовлеченная в движение; u - скорость движения среды.
Здесь сила F - есть разность напряжений σ-σ0, в виде скачка напряжений, который растягивается во времени t, при начальном σ0—>0, тогда импульс равен:

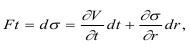
где r - текущая координата расстояния.
В свою очередь то же импульс, выраженный через массу и скорость, равен:

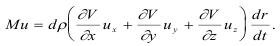
Отсюда закон сохранения импульса выразится как:

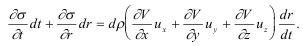
В соответствии с последним соотношением в результате прохождения волны на расстоянии r от заряда общее количество движения, приобретенное средой, не должно превышать величины, определенной законом сохранения импульса.
Закон сохранения энергии. Энергия Wo, внесенная в среду волной напряжений, расходуется на изменение внутренней энергии системы при сохранении баланса:

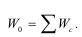
Потенциальная энергия взрывчатого разложения BB определяется теплотой химического разложения:

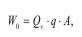
где Qv - теплота разложения BB, ккал/кг;
q - масса заряда;
А - механический эквивалент тепла, 427 кгм/ккал.
Абсолютное значение энергии во фронте волна напряжений определяется условиями распределения энергии на расстоянии r за время dt.
В балансе энергии ∑Wc представляет:
- необратимые потери в виде теплового рассеивания и упругие колебания среды;
- упругие и пластические деформации горных пород от волны напряжений;
- энергия образования новых поверхностей при возникновении и росте микротрещин и нарушение сил внутреннего сцепления породы;
- кинетическую энергию перемещающихся масс;
- энергию образования микротрещин, смыкающихся после снятия волны напряжений.
Отсюда баланс энергии будет выглядеть как:

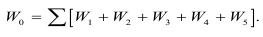
В настоящее время выделяют два основных направления в трактовке механизма разрушения горных пород взрывом.
Первое направление представляет процесс разрушения под действием системы сил, при которой достигаются усилия напряжений превышающих максимум сил сцепления, причем само напряженное состояние среды может быть разнообразным - от усилий сжатия, до растяжения и сдвига, и проявление этих усилий может быть одно- и многоосно, кратковременно или длительно. Отсюда достижение максимума сил сцепления может произойти раньше или позже теоретического максимума.
Система тотальной неопределенности исходных условий и параметров не позволяют построить законченную картину процесса разрушения.
По второму направлению, процесс разрушения горных пород является не результатом достижения напряжения, превышающего максимум, а результатом накопления внутри среды определенного запаса упругой энергии, при которой дальнейшее существование двух или более частей тела является более целесообразным, чем одной, что можно описать формулой:

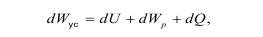
где dWyc - изменение упругой энергии среды, расходуемое на образование новых поверхностей, а также кинетической энергии движения частиц среды и энергии теплового рассеивания;
dU - поверхностная энергия образования новых поверхностей (энергия дробления);
dWp - кинетическая энергия движущихся масс;
dQ - энергия теплового рассеивания.
Теория максимальных напряжений (первое направление). Хрупкое разрушение горных пород наступает при напряжениях в среде, которые превышают силы сцепления. Кратковременный и резко изменяющийся во времени и пространстве характер напряжений свидетельствует, что в зоне, примыкающей к заряду, имеется зона сжатия, т.е. σmax>0 и σmin>0. Достижение волной напряжений свободной поверхности приводит к образованию условия σmax>0 и σmin0,992-0,995, т.е. объем после взрыва должен увеличиться всего на 0,008-0,005.
Модуль всестороннего сжатия связан с физическими константами пород:

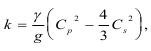
где Cp и Cs - скорость продольной и поперечной волны соответственно; γ - плотность среды; g - ускорение силы тяжести.
Существует некоторая критическая энергия разрушения, которая может быть определена на основе теории дробления, когда число частиц n соответствует степени дробления:

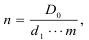
а удельная работа дробления равна:

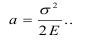
Энергия дробления изменяется как показатель степени числа частиц n и пропорциональна lgn:

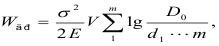
где D0 - максимальный линейный размер среды до взрывания;
dl, dm - средний линейный размер частиц определенного класса крупности, установленный гранулометрическим анализом;
m - количество классов крупности;
E - модуль Юнга;
σ - сопротивление разрушению среды.
Рассмотрим изменение объема среды как частную производную в виде:

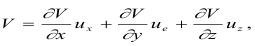
где ux, uy, uz - скорости деформирования объема V0 до V.
Поскольку скорость нагружения по одной оси связана с акустической жесткостью λ=Срρ соотношением:

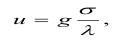
то объем деформации составит:

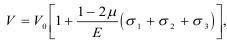
где Е и μ - модуль упругости и коэффициент Пуассона.
Эти показатели можно определить из теории упругости по соотношениям:

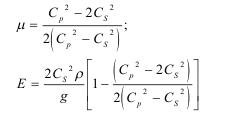
В этом случае объем разрушений составит:

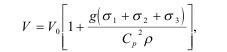
здесь ρC2p=G - динамическая жесткость среды.
Преодоление сил упругой и пластической деформации до образования трещин еще недостаточно для производства выемки и погрузки разрушенной горной массы и ее транспортирования, что является безусловными процессами разработки месторождений. Вероятно, энергия разрушения должна быть дополнена энергией на некоторое сдвижение массива горных пород.
Отсюда возникает необходимость учета траектории движения масс по законам внешней баллистики, и тогда общие затраты энергии на перемещение составят:

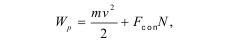
где Wp - кинетическая энергия перемещающихся масс;
m - масса разрушенной породы;
v - средняя скорость движения частиц по баллистической кривой;
Fcoп - сопротивление воздуха движению массы;
N - длина баллистической кривой.
Если учесть, что m можно получить интегрированием до некоторого объема V2 от объема V1, а для определения силы сопротивления воздуха требуются довольно сложные выражения, то установление Wp становится громоздкой задачей.
В.Н. Мосинец предлагает более простой путь, когда для определения кинетической энергии перемещения в качестве скорости следует принять критическую скорость разрушения среды Co, которая в начале всегда выше средней скорости движения:

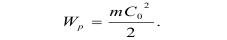
Если иметь в виду, что масса m, перемещающаяся в воздухе равна:

где к=V2/V1 - коэффициент разрыхления породы, то затраты энергии на перемещение составят:

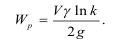
Кроме энергии, идущей на разрушение (дробление) Wдр и на перемещение разрушенных частиц Wp, значительная часть энергии взрыва расходуется на диссипативные потери (нагревание, рассеивание и др.), однако их доля незначительна и составляет 5—12% в зависимости от показателей G и λ. Другая, более заметная часть энергии, содержится в сейсмической волне, достигая 35-55% от потенциальной энергии BB, установление возможных путей использования которой является очень важной задачей.

---