Моделирование механизма разрушения твердых тел

Напряженно-деформированное состояние, связанное с образованием соответствующих зон, характеризуется также различными остаточными деформациями различной интенсивности, например, зонами разрушения, заколами, сдвигами. Эти явления находятся в прямой зависимости от энергии взрыва и обратно пропорциональны свойствам среды.
И.Ф. Оксанич и П.С. Миронов рассматривают процесс разрушения как систему частиц движущихся с различными скоростями в одном направлении до и после разрушения, а наибольшая разница в скоростях находится вблизи поверхности. Здесь скорость смещения удваивается. В результате влияния градиента скоростей возникают критические деформации и нарушение сплошности массива.
Для проверки этих утверждений нами выполнено моделирование на плоских моделях из оргстекла. Оригинальная методика проведения экспериментов позволила доказать наличие градиента скоростей и их векторную картину.
Методика экспериментов включала взрывы зарядов ТЭНа в патрончиках диаметром 2 мм при плотности заряжания 0,6 г/см3 на плоской модели уступа с определенным углом откоса. Предусматривалось проведение шести серий опытов в следующих вариантах:
- при прямом и обратном инициировании зарядов;
- при наличии торцовой стенки скважины (запертыми продуктами взрыва);
- при отсутствии торцовой стенки, когда продукты взрыва могли свободно отходить от модели уступа;
- при имитации нетрещиноватой среды (кусочки оргстекла приклеены к откосу в различных его точках клеем, способным передавать сдвигающие напряжения);
- при имитации трещиноватого массива (кусочки оргстекла на плоскости откоса не приклеивались).
Опыты, проведенные на оргстекле для выявления влияния откольных явлений на кинематические параметры перемещающихся частей уступа, показали следующее.
В том случае, когда кусочки лежали свободно, имитируя модель трещиноватой среды, во всех случаях взрывания, а именно, независимо от соотношения скорости детонации и скорости продольной волны напряжений и направления детонации, кусочки движутся по нормали к поверхности откоса, угол которой с горизонталью определяется самим углом откоса ψ.

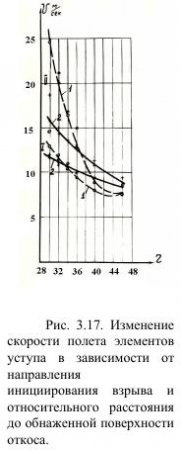
Величина средней начальной скорости полета элементов уступа по его высоте изменяется только в зависимости от относительного расстояния, (рис. 3.17), что для зарядов ТЭНа выражается соотношением:

где v - скорость полета, м/с; r - относительное расстояние в диаметрах заряда.

Эксперименты подтвердили, что в случае наличия предразрушения в виде трещин, которые пропускают через себя только нормальную составляющую напряжений, направление движения частиц среды определено положением поверхности раздела, а величина скорости зависит только от условий затухания интенсивности напряжений с расстоянием.
В случае закрытого заряда направление векторов скорости остается без изменений, величина ее, как правило, возрастает в два раза, что объясняется действием прорывающихся продуктов взрыва, закон изменения величины скорости имеет тот же вид. Результаты опытов с приклеенными кусочками, имитирующими монолитный массив, показали удовлетворительную сходимость при более высоком уровне величин скоростей. Увеличение скоростей можно объяснить наложением вертикальной составляющей, обусловленной действием прямых и отраженных волн с вертикальной компонентой скорости, определяемой действием скалывающих напряжений. Последнее не противоречит закону сохранения количества движения, что должно привести к росту скорости.
Анализ результатов серийных экспериментов показал, что при постоянном угле откоса Ψ угол вылета пилот-куска зависит от соотношений, а также упругих постоянных среды, в частности от коэффициента Пуассона:

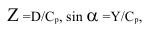
где α - угол падения волны напряжений; Y - текущая ордината, определяемая положением верхнего торца заряда.
Если считать, что соотношения постоянны во все время процесса, то применительно к откосу уступа, угол падения волны не является постоянным и зависит от положения наблюдаемой точки. Этот принцип определяет факт вылета кусочков под различными углами.
При одном направлении инициирования и закрытом, а также открытом зарядах, углы вылета одинаковы, отклонения от среднего не более 5%. В табл. 3.2 приведены углы вылета пилот-куска и углов падения волн напряжений (рис. 3.18 а, б).

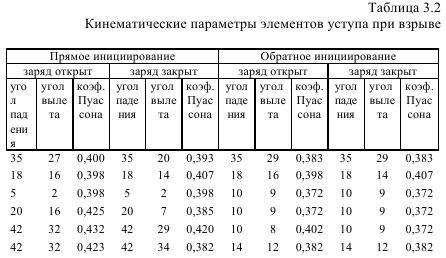
Из данных табл. 3.2 следует, что верхняя треть уступа в обоих случаях движется под одинаковыми углами, т.е. направление инициирования не изменяет результата в направлении полета при Z>1 и sinα=const. Остальные 2/3 уступа в зависимости от направления инициирования, имеют совершенно различные углы, а для обратного инициирования эти направления достаточно близки. Направление полета полностью определяется местом инициирования. Эксперименты с закрепленными кусочками при одинаковых относительных расстояниях r=R/d с приходом волна под углом, изменяющимся в широких пределах показали, что скорости полета зависят от угла падения волны, это выражается уравнением:

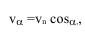
где vn - скорость при падении волна под прямым углом к поверхности.
Тогда влияние угла падения на величину скорости определяется соотношением:

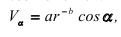
где r - относительное расстояние, R/d.

При обратном инициировании в нижних 2/3 уступа градиент снижения скорости меньше, что обусловлено малыми углами падения волн напряжений и это непосредственно сказывается на худшем разрушении среды. В случае закрепленных кусочков изменение скорости может быть описано выражением:

Для закрепленных кусочков абсолютная величина скорости как в случае открытого, так и закрытого заряда выше, чем для незакрепленных на 85%, что объясняется влиянием вертикальной составляющей волны напряжений. Для заданного угла откоса, при достаточно широком диапазоне углов падения волны (0-40°), величина скорости колеблется всего в пределах 23% в сравнении с величиной нормальной составляющей, в то время как для относительных расстояний, изменяющихся в пределах до 5 r, изменение скорости наблюдается до ±50%.
Покадровый анализ сверхскоростной киносъемки с помощью СФР показал удовлетворительное совпадение значений скоростей по установленным зависимостям. В табл. 3.3 приведены величины скоростей полета частиц, при этом начальные скорости в первые 37 мкс мало отличаются от средних скоростей, установленных при дешифрировании кинокадров от камеры CKC-1 м.

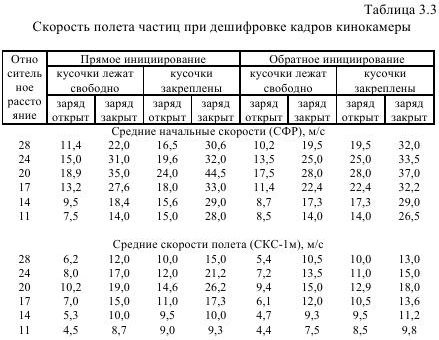
Используя известные соотношения теории упругости, связывающие массовые скорости движения массива, напряжения во фронте волны, установлены предельные сопротивления отрыву в эксперименте в сравнении с табличными данными. Они оказались полностью совпавшими (учитывая разрешительную способность киноаппаратуры). В частности, вычисленное временное сопротивление отрыву оказалось равным 56,7 МПа, в то время как в табл. 3.4 указано около 55 МПа.
Разрушающее напряжение отрыву соответствовало скорости полета около 44,5 м/с, а массовая скорость - 23 м/с, которую можно принять за критическую скорость разрушения.
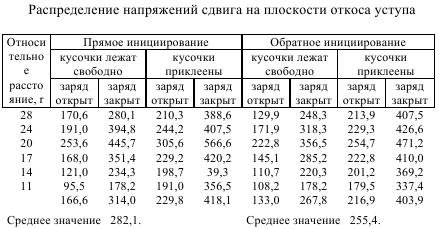
Представляет интерес распределение величин сдвиговых напряжений по плоскости откоса (в кг/см2), рассчитанных по известной формуле теории упругости (табл. 3.4).
Анализ поля скоростей на поверхности откоса и сопоставление их с зонами разрушения по местам локализации затемненных областей, свидетельствующих об их разрушении, полностью подтверждает высказанное предположение, что в разрушении особую роль играет не только абсолютная величина критической скорости, но и ее направление. Так, если в середине откоса имеем высшие скорости полета (по модулю), но небольшие углы фронта волна сдвига с нормалью к свободной поверхности, то в нижних частях при невысоких скоростях наблюдаются большие значения этих углов. Таким образом, на основании изложенного выше материала, можно сделать следующие выводы.
1. Для пород, обладающих средней и высокой акустической жесткостью (10*10в5 - 25*10в5 г/см3см/с), направление полета частей уступа определяется суммарным воздействием прямых, отраженных и волн сдвига. Продукты взрыва не оказывают влияния на векторную картину скоростей из-за из запаздывания с воздействием.
Величина скорости зависит от угла падения волн напряжений и относительного расстояния от оси заряда до свободной поверхности, причем влияние последнего фактора проявляется в большей степени, чем углов падения волн.
2. Параметрические свойства BB и физико-механические показатели среды влияют на величину скорости, а также на направление смещения элементов уступа. Так как кровля нижележащего горизонта разрушена зарядом в перебуре скважин вышележащего, то под действием взрыва зарядов BB в нижележащем горизонте траектории движения кровли полностью подчиняются закономерностям, установленным выше для трещиноватой среды, что позволяет по величине смещений точки поверхности восстановить траектории всех частей вглубь массива.
3. Для пород с низкой акустической жесткостью (0,5*10в5 -10*10в5 г/см3, см/с), разбитых густой сетью трещин, направления полета соответствуют направлению лучей прорыва продуктов детонации к свободной поверхности. Величина скорости определяется количеством движения, заключенного в продуктах взрыва и распределения его вдоль оси и стенок скважины.

Остаточные деформации визуально наблюдаются в виде заколов в тыл массива, распространяющихся трещин различного направления и т.п. Так уходка понизу и поверху от последнего ряда скважин, зависящая от величины зарядов, сопротивления по подошве, числа рядов скважин и свойств пород, колеблется понизу от 0,5 до 1 м, а поверху - 5-8 м, правда это произойдет при взрыве на свободной поверхности откоса уступа.
Наибольшие нарушения в тыл от взрыва наблюдаются вблизи кровли, где степень раскрытия трещин и их частота уменьшаются с удалением от последнего ряда скважин, и в глубину трещины образуются параллельно взрываемому блоку. На расстоянии 30 м деформации составили 6-7 мм на расстоянии 20 м - уже 15 мм.

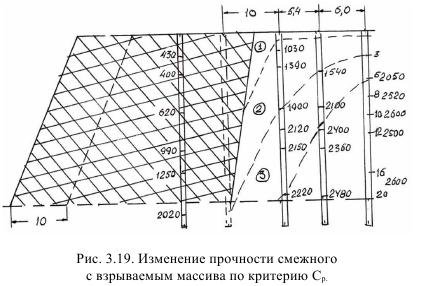
Сопоставляя рис. 3.19 с рис. 3.6 по зондированию взорванного и прилегающего к взрыву объемов массива с помощью прозвучивания (по Cp), можно констатировать их полную идентичность. За пределами области дробления в зоне остаточных деформаций прослеживаются несколько систем трещин. Первая -типа заколов, обнаруживается на расстоянии 9 м от линии отрыва максимальной шириной 0,5 м, на густо разбита трещинами радиального направления. Вторая - глубиной менее 0,2 м на расстоянии 9-15 м от линии отрыва и радиальных трещин здесь мало, третья система - длиной до 3 м и шириной менее 3 мм, где радиальные трещины вообще отсутствуют.
Вместе с тем имеются сведения, что при взрывании вертикальных скважин трещины проявляются на расстояниях 30 м, а иногда и 60 м от последнего ряда скважин при их ширине 0,1-0,6 м и длиной 10-15 м, но с удалением их ширина уменьшается, как и их длина. При использовании вертикальных скважин диаметром 200-250 мм нарушения прослеживаются на расстоянии до 70-75 м.
Постепенное исчезновение радиальных трещин свидетельствует о снижении интенсивности тангенциальных растягивающих напряжений. Чем слабее породы, тем дальше от линии отрыва отстоят все системы трещин, а последняя может оказаться на расстоянии до 60 м.
Обращает на себя внимание тот факт, что остаточные деформации в виде трещин находятся в прямой зависимости от диаметра зарядов. Так, зона дробления полностью соответствует W, зона больших заколов с трещинами шириной более 3 мм - 1,5W, зона мелких трещин до 3 мм - 3,5-4W, а зона микротрещин до 8-10W. Если иметь в виду, что W=f(d), то совершенно понятна прямая зависимость от диаметра заряда, характера и интенсивности зон трещинообразования в тыл массива, в целом характеризующая степень разупрочнения его в результате взрывов на соседних участках.

---