Физические основы процесса разрушения (теории трещинообразования)

Положения современной физики твердого тела дают представление о явлении разрушения с учетом его атомномолекулярной структуры, позволяющей развить статистическую теорию прочности и разрушения, которая, тем не менее. He обходится без использования энергетического принципа в объяснении концепции нарушения сплошности среды.
Процесс трещинообразования не всегда приводит к разрушению тела, в понимании полного распада на отдельности, т.е. трещины могут и не пересекаться. Однако трещинообразование является причиной разупрочнения или предтечей разрушению. Поэтому теория трещин приводится в этой части книги.
Разрушение как процесс связывается с дефектами кристаллической решетки или самих кристаллов, при этом размеры этих дефектов в пределах макроскопических параметров тела могут рассматриваться на различных уровнях. В совокупности различные размеры дефектов и места их концентрации в теле обусловливают его структурные неоднородности. Некоторые одномерные дефекты, объединенные в цепи, образуют неоднородности в виде дислокаций. На основании теории дислокаций и возможности их перемещения в виде скольжения атомных слоев, можно объяснить образование микротрещин и, наконец, разрушение твердого тела.
Движение незакрепленной дислокации сопряжено с сопротивлением трению, а это значит, что на дислокации действуют лишь касательные напряжения. Затрудненное движение, т.е. торможение роста трещины за счет увеличения сопротивления трению говорит о преобладании пластических свойств.
Описать процесс разрушения можно с позиций квантовой механики, т.е. используется фононная концепция (Бартеньев, Разумовская), где под фононом понимается квант поля колебаний кристаллической решетки. Здесь дефекты рассматриваются как области концентрации напряжений с особым фононным спектром, отличающимся от такого же спектра всего нагруженного тела. Область перенапряжений есть полупрозрачный резонатор, испускающий колебания, раскачивающие неравновесное состояние тела через рост дефектов, их срастание и образование трещин.
Теория разрушения Гриффитса основана на энергетическом методе описания этого процесса. Его последователи со своими вариантами теории (Смекал, Ирвин, Орован и др.) также придерживались этой концепции.
Предположение Гриффитса о наличии дефектов в ненагруженных телах, позволило ему представить область концентрации напряжений при нагрузках. Эта область представляется в виде эллипса с величиной напряжений у вершин, равными:

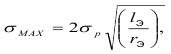
где σр - растягивающее напряжение;
1э - длина большой полуоси эллипса;
rэ - радиус кривизны на концах большой полуоси эллипса.
На самом деле rэ стремится к 0 и тогда σмах стремится к бесконечности.
Потенциальная энергия упругого тела, сдерживающая трещину, имеет три составляющие:
1) энергию упругой деформации тела, кроме того участка, где имеется трещина;
2) энергию упругой деформации, связанная с трещиной Eε и благодаря которой трещина существует;
3) поверхностную энергию образования трещина Es.
Наличие малых трещин и дефектов в материале по теории Гриффитса означает, что фактическая его прочность ниже, чем расчетная и обусловлена некоторым критическим напряжением, сосредоточенным на конце трещины:

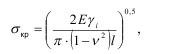
где E - модуль упругости;
γi - плотность поверхностной энергии;
v - коэффициент Пуассона;
l - длина трещины.
Для плоского напряженного состояния предыдущее выражение представляется в виде:

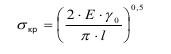
Б.Я. Пинес, исходя из теории размерностей и подобия, для объемного напряженного состояния нашел, что:

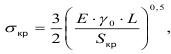
где L - линейный размер тела; Sкр - площадь трещины.
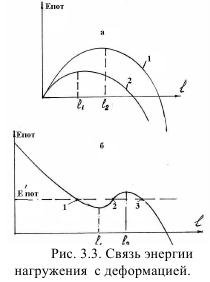
Я.И. Френкель обнаружил существенное противоречие между гипотезой Гриффитса о наличии дефектов в теле ненапряженного состояния и используемым при этом уравнении энергетического баланса. По этому уравнению в таком теле существовать микротрещины не могут, и тогда это противоречие сводится к тому, что на кривой Епот (1) должна быть одна экстремальная точка (рис. 3.3а), которой соответствует максимум энергии, т.е. тело находится в устойчивом состоянии. На самом деле некоторые ученые, получив полное уравнение энергетического баланса обнаружили, что Eпот (1) может быть по кривой рис. 3.3б. То есть таких устойчивых состояний может быть несколько, что вполне соответствует теории катастроф, когда и при меньших напряжениях тело может разрушиться.

Г.Р. Ирвин и О.Е. Орован в теории квазихрупкого разрушения также учитывают энергию пластической деформации, т.е. заменив в формуле Гриффитса у на эквивалентную поверхностную энергию γэф, как сумму действительной поверхностной энергии и энергии пластической деформации.
Н.Ф. Мотт на основании анализа размерностей получил выражение для кинетической энергии, движущейся трещины:

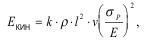
где v - скорость распространения трещины;
k - безразмерный коэффициент;
σр - растягивающее напряжение.
Далее дополнив уравнение энергетического баланса, он нашел скорость роста трещины:

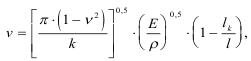
где 1k - критическая длина трещины.
Если скорость распространения трещины предельная и равна скорости волны Рэлея, т.е. около 0,63Ср (скорости продольно волны), то скорость роста в этом случае равна:

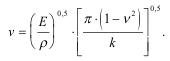
Факт разрушения твердого тела говорит о том, что этот процесс явно необратимый. Рассмотрим этот тезис с позиций того же баланса энергии, для чего нужно сразу признать, что поверхностная энергия тел является не потенциальной, а свободной энергией. Для образования новой поверхностной свободной энергии не обязательно выполнение условий изотермичности, т.е. при T=Const работа процесса выражается как:

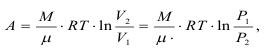
где M - масса газа;
μ - молекулярная масса;
R - газовая постоянная;
T - абсолютная температура;
V2 - объем начальный;
V1 - объем конечный;
P1 - начальное давление;
P2 - давление конечное.
Согласно принципу Ле-Шателье, при нагревании площадь поверхности тела увеличивается и, значит, любое увеличение этой площади другими способами (кроме нагревания) приведет к понижению температуры поверхности. Теперь уже экспериментально доказано, что температура вновь образованной поверхности ниже, чем температура внутренних точек тела, т.е. присутствует необратимый тепловой поток от внутренних точек тела к внешним.
Согласно второму началу термодинамики, куда входит теорема о минимуме потенциальной энергии в неявном виде, второй закон сохранения энергии выглядит как:

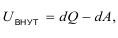
где Uвнут - внутренняя энергия системы;
Q - количество теплоты, полученное системой;
А - работа, выполненная системой.
Второе начало термодинамики представлено известной формулой:

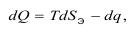
где Sэ - энтропия; q - диссипированная энергия.
Гельмгольц связь между внутренней энергией и свободной сводит к выражению:

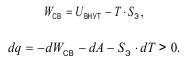
Так как приращение свободной энергии связано с увеличением длины трещины по Гриффитсу, то:

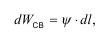
где ψ - поверхностная энергия трещины, приходящаяся на единицу ее длины.
Приращение упругой энергии составит:

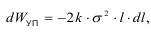
где к - постоянная.
Диссипированная энергия выразится следующим образом:

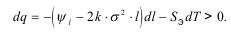
Теорема Гриффитса верна при SэdT→0, но это верно лишь при температурах, близких к абсолютному нулю.
Если обратить внимание на возражение Я.И. Френкеля по поводу некоторых противоречий с уравнением энергетического баланса и в соответствии с рис. 3.2, то трещина может расти и тогда, когда энергия деформации в окрестностях критической точки будет уменьшаться и даже больше, чем та, которая требуется для упругой деформации, доведенной до разрыва. На это обратил внимание И.И. Бикерман. В отличие от теории Гриффитса Бикерман полагает, что энергия, затрачиваемая на разрушение переход в теплоту, а не в поверхностную энергию трещины, тогда следует вместо энергии разрушения использовать удельную работу разрушения, с иным физическим смыслом.
Попытка описать процесс разрушения с позиций квантовой механики, где под фононом понимали квант колебаний, поддержана И.В. Криггсом. Он предполагал, что разрушение в целом явление квантовое, т.е. прерывистое. В дальнейшем это будет доказано экспериментально, когда разрушение твердого тела взрывом происходит скачкообразно о чем свидетельствует прерывистое поведение фрактальной размерности. Криггс полагает, что атомные связи рвутся в пределах ограниченной площадки F3 за небольшой промежуток времени, а так как трещина не может расти со скоростью больше скорости продольной волны Cp, то и энергия новой поверхности сосредоточена на ограниченной поверхности, распространяющейся от краев трещины на расстояние a=CpΔt.
Роль энергии упругих деформаций состоит в том, что она должна быть больше некоторых сил сцепления в объеме тела:

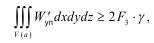
где W'уп - энергия упругих деформаций на единицу объема V(a), равного области сосредоточения энергии.
В случае разрушения кристалла одноосным усилием σр, то оно эквивалентно силам сцепления, приходящимся на единицу площади, и тогда приведенное выше уравнение сводится к виду:

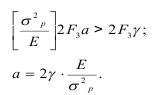
Последнее соотношение представляет собой необходимое и достаточное условие для разрушения твердого тела, a F3 - является функцией его внутренней структуры, связанной с размерами кристалла или зерна.
В теории Гриффитса и ее модификациях особое место отводится тупиковой части трещины - месту скопления напряжений.
Это положение позволило представить так называемый силовой подход к описанию процесса разрушения путем замены сил сцепления, которые действуют в конце трещины на внешние силы. В такой интерпретации задача распространения трещины может быть решена как силовая концепция механики деформируемого тела.
В работах наших земляков М.Я. Леонова, В.В. Панасюка и других предложена иная модель твердого тела, имеющего микро- и макротрещины. В основу модели положено предположение, что существует зависимость сил сцепления от расстояния, т.е. промежутка между берегами трещины. Если это расстояние δк меньше некоторой постоянной величины, являющейся константой для данного материала, то силы притяжения между берегами также будут равны постоянной величине σ0. В случае, если фактическое расстояние между берегами больше δк, то σ0=0.
Эта концепция означает, что трещина будет расти, если выполняется условие:

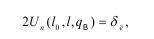
где Uп - нормальная составляющая вектора смещений точек берегов трещины;
l0 - характерный линейный размер области начальной трещины;
l - фактический размер трещины;
qв - параметр, зависящий от внешней нагрузки.
Основной идеей статистической теории прочности (С.Д. Волков) является построение такой модели среды, которая позволяет использовать методы математической статистики при описании процесса разрушения. Модель квазиизотропного кристаллического тела представлена однофазной системой, в объеме Wv которого кристаллы связаны силами сцепления. Величина Wv должна быть такой, чтобы условно считалась однородной. Внутри этого объема имеется малый объем V существенно меньше всего тела, но все же имеющий достаточное количество элементарных частиц, т.е. Wv>>V.
В теории трещинообразования выделяют различные условия нагружения твердого тела, чтобы образовались микротрещины и макротрещины. Первые, в представлении М.В. Якутовича, образуются под действием растягивающих напряжений и, даже в случае сложного напряженного состояния, рассматривается только нормальная составляющая напряжений растяжения. Процесс макроскопических разрушений в масштабе V-объемов начинается при напряжениях меньше сопротивления разрушению поликристаллов.
Относительное число разрушенных объемов V, где микротрещины возникли под действием одноосного растягивающего напряжения ст, равно:

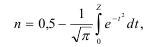
где z равно:

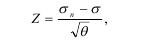
σп - среднее сопротивление разрушению кристаллов поликристаллического тела; θ - модуль нормального распределения объемов V по напряжениям.
С увеличением внешней нагрузки число разрозненных микротрещин возрастает и, после достижения некоторой критической величины nкр, они начинают сливаться в единые, в том числе и пересекающиеся, образуя макроскопическую трещину во всем объеме Wv. Условием достижения критического числа микротрещин при любом напряженном состоянии тела является равенство:

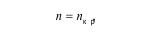
где nкр - постоянная для данного материала величина, равная относительному числу трещин в объемах V, достаточному для макроскопического разрушения тела объемом Wv.
Твердый материал, как известно, при разрушении может вести себя хрупко или пластично. Макроскопическим разрушением обычно охвачены не все объемы Wv, а только их некоторая часть. Чем материал более хрупок, тем эта часть меньше, поскольку в хрупком материале микротрещины опаснее, чем в пластическом. В процессе макроскопического разрушения в малых объемах V разрушение может быть вязким, а соотношение объемов Vi между хрупким и вязким разрушением определяется характером макроскопического разрушения. Из этого следует, что в общем случае под действием внешних усилий в разрушаемом теле возникают как упругие, так и пластические деформации.
Из общего числа N объемов типа V часть их Ny -деформируется упруго, a Nп - пластично. Общее число микротрещин к моменту макроскопического разрушения составит:

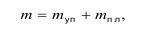
где mуп и mпл - число микротрещин при упругом и пластическом деформированных объемах соответственно Vуп и Упл.
Относительное число микротрещин составит:

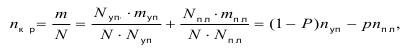
где Nуп/N = p - вероятность пластического состояния; nуп и nпл - относительное число микротрещин в пластически и упруго деформированных объемах V соответственно.
Критериями хрупкого и вязкого разрушения статистической теории прочности являются условия:

При этом следует также иметь в виду, что как уже экспериментально доказано Г. Кольским, хрупкость материала зависит от скорости приложения нагрузки и физико-механических свойств горных пород.

---