Основы теории подобия и размерностей

Моделирование, как метод познания, применяется в том случае, когда какие-либо явления или процессы не могут быть описаны уравнениями физики или математики вследствие их сложности. При моделировании процесс воспроизводится на модели, сходной с натурой, при этом она меньше последней.
Моделирование бывает физическим, когда объектом его являются материальные модели, а также математическим, объектом которого является математическая зависимость или идеальная модель.
При физическом моделировании модели могут быть изготовлены из материала натуры или совершенно другой физической природы, такие материалы называют эквивалентными.
Целью моделирования является обнаружение закономерностей поведения модели в ходе процессов и возможность переноса их на натуру, при этом сам перенос осуществляется с помощью переходных коэффициентов, определение которых является результатом простых вычислений.
В развитии моделирования можно выделить три этапа. Первый - это Ньютоновская формулировка первой теоремы о механическом подобии, чем последовало установление критериев подобия различных механических систем, например, критерий Эйлера для прочных конструкций. Аналогично этому, критерий Бартона - для описания подобия механических движений, Кирпичева - подобия упругих явлений, а в гидродинамике — критерии Рейнольдса, Фруда, Коши и т.д. Второй этап - это формулировка π-теоремы, т.е. основной теоремы о возможности выражения физических законов в виде зависимостей между критериями подобия, которые являются безразмерными величинами. Третий этап - формулирование третьей теоремы М.В. Кирпичевым и А.А. Гухманом о возможности распространения результатов единичного опыта на группы явлений: «подобными явлениями будут те, которые имеют подобные условия однозначности и одинаковые определяющие критерии». В настоящее время нет ни одной области науки и техники, где бы ни применялось моделирование, что объясняется дешевизной метода в сравнении с другими.
Масштаб модели во многом определяет стоимость исследований, и эти масштабы могут быть разными. Например, туннель сечением в 100 м2 в масштабе 1:50, составит 2 м2, а крейсер длиной 250 м - 5 м. Применительно к горному делу при проектировании каменно-набросной плотины Камбаратиской ГЭС предусматривались исследовательские работы с модельным взрывом в 740 т ВВ.
Критерии подобия могут быть получены при анализе размерностей физических величин. Единицы измерения образуют систему единиц, куда входят независимые и зависимые параметры. К независимым в системе СИ относятся:
- масса (кг) [М],
- длина (м) [L],
- время (сек) [Т],
- сила тока (а),
- температура (К0),
- сила света (св).
Все остальные могут быть выражены через эти параметры, и они являются зависимыми (производными).
Для примера рассмотрим уравнение второго закона Ньютона:

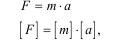
т.е. если известны размерности двух величин, то можно определить размерность третьей. Развернем это утверждение:

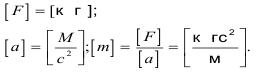
Значит, при «n» физических величин и известных первых «К» размерностях размерности остальных величин «n-k» - будут производными.
Отсюда формулировка Пи-теоремы: «Любое уравнение, связывающее между собой N физических величин, среди которых К величины обладают независимыми размерностями, может быть преобразовано к уравнению, связывающему N-K безразмерных комплексов и симплексов, составленных их этих величин».

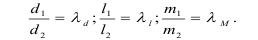
Симплексы - это отношение двух одноименных величин, т.е. с одинаковыми размерностями:
Комплексы служат критериями подобия и они обычно являются степенными комплексами.
Понятие о критериях подобия можно получить, продолжая анализировать уравнение второго закона Ньютона.
Предположим, что имеем две подобные между собой системы:

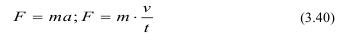
Выразим все переменные второй системы через переменные первой:

Подставим их во вторую систему:

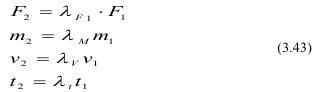
Тождественность (3.41) и (3.44) будет, если:

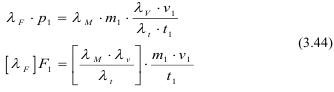
Из (3.45) вытекает, что:

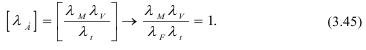
В теории подобия критерий обозначается следующим образом:

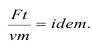
Он является безразмерным, а все λм, λt, λF, λv являются масштабными коэффициентами или симплексами:

Теория размерностей определяет число критериев-комплексов и критериев-симплексов следующим образом.
Если явление или процесс описывается уравнением, куда входит N всех величин, а число величин с неодинаковыми размерностями п, и число величин с независимыми размерностями К, то число критериев комплексов равно:

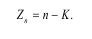
Число критериев-симплексов равно:

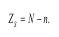
Общее число критериев равно:

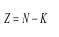
Основным смыслом моделирования является возможность трансляции результатов опытов с моделями на натуру. Такая возможность обеспечивается доказательством того, что натура и модель подобны, т.е. подчиняются одним и тем же физическим законам или описываются одинаковыми математическими зависимостями.
Два явления или процесса подобны, если по заданным характеристикам одного можно определить характеристики другого при помощи переходного коэффициента (масштаба).
Подобие различают:
- геометрическое - идентичность формы объектов натуры и модели. Геометрический масштаб — это соотношение двух любых линейных размеров модели и натуры;
- кинематические - идентичность скоростей, времени протекания процесса на модели и в натуре;
- динамическое подобие — идентичность силовых полей, ускорений, масс.
Механические перемещения базируются на кинематическом подобии. Это означает, что положение объекта в натуре и модели, определяемое координатами точек в функции времени будет подобным и отношение координат аналогичных точек для сходственных моментов времени являются константой:

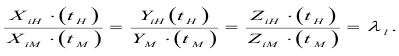
Величина скорости определяется соотношениями:

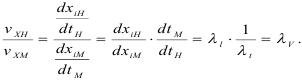
Аналогично и для ускорений:

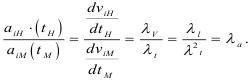
При исследовании силового и энергетических полей, кроме кинематического подобия, должны быть подобны материальные системы, тогда обеспечивается динамическое подобие:

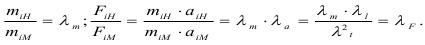
Подобие выполняемых работ определено соотношением:

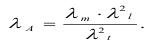
Действие взрыва в твердом теле сопровождается следующими явлениями:
а) детонацией заряда;
б) истечением продуктов взрыва;
в) механическим воздействием продуктов детонации на среду;
г) распространением волн напряжений в среде;
д) разрушением среды;
е) сдвижением разрушенного материала и разлетом осколков. При рассмотрении явления детонации системой является заряд BB, изменяющий свое состояние. В ходе химической реакции меняются величины:
- температура (T°K);
- плотность (ρ);
- давление (P);
- объем прореагированного вещества BB (V);
- скорость смещения частиц в ударной волне (U);
- скорость звука в продуктах детонации (С).
В то же время сама система (заряд) имеет свои элементы:
- диаметр заряда (d);
- длина заряда (l);
- плотность заряжания (Δ);
- скорость детонации (W);
- удельная энергия BB (E).
Параметрами истечения продуктов детонации являются:
- скорость истечения (uпд);
- плотность истекающих продуктов (ρпд);
- давление (Pпд);
- температура (Тпд).
Параметрами системы являются:
- диаметр заряда (d3);
- первоначальная плотность заряда (ρ3);
- температура продуктов детонации (Tпд);
- давление продуктов детонации (Pпд);
- объем продуктов детонации (Vпд);
- коэффициенты сопротивления движению продуктов детонации.
Процесс взаимодействия продуктов взрыва и среды описывается соответствующими параметрами двух процессов, перечисленных выше, а также и углом встречи ударной волны со стенкой среды (зарядной камеры).
Явление распространения волны напряжений сопровождается изменением напряжений в различных точках среды. Системой в данном случае является среда, а ее характеризует состояние, описываемое параметрами:
- величина напряжений и деформаций в точке (σ, ε);
- положение фронта волны напряжений (хi);
- напряжение на фронте волны (σв);
- плотность среды (ρс);
- температура (Tc).
Параметрами системы являются:
- скорость распространения волны напряжений (Св);
- коэффициент диссипативных потерь (кп);
- первоначальная плотность среды (ρс);
- модуль упругости (E);
- коэффициент Пуассона (μ);
- пористость (n);
- динамическая сжимаемость (G).
Разрушение хрупкого материала есть нарушение сплошности среды. Процесс характеризуется следующими параметрами:
- изменение поля напряжений (σн);
- размер трещин (1тр);
- скорость развития трещин (vтр);
К параметрам системы относят:
- прочность материала (σс);
- модуль упругости (E);
- скорость разрушения (vтр);
- энергоемкость разрушения (е);
- распределение микротрещин по размерам (n%).
Сдвижение породы и разлет кусков — это процесс перемещения и его параметры следующие:
- скорость (vп);
- ускорение (ап);
- направление (х, у).
Параметрами системы будут:
- масса кусков (Мк);
- коэффициент сопротивления движению (Kсоп).
Анализ параметров всех процессов свидетельствует, что их можно сгруппировать. Для примера рассмотрим распространение одномерной упругой волны, т.е. параметры процесса и системы:
- скорость волны С;
- скорость смещения среды v;
- величина смещения u;
- расстояние до точки наблюдений r;
- время пробега волны t;
- модуль упругости Е;
- напряжение σ;
- модуль Пуассона μ;
- плотность среды ρ.
Согласно Пи-теореме имеем общее число параметров N=9, а число единиц К=3, тогда число критериев подобия составит:

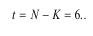
Среди них имеем:
1. П1=μ, так как коэффициент Пуассона в модели равен коэффициенту в натуре.
2. П2=Е/σ; 3. П3=r/u; 4. П4=u/vt; 5. П5=σ/ρС2; П6=Е/ρС2.
Имея в виду, что: rн/rм=λ1; ρн/ρм=/λp; tн/tм=λt - соответственно масштабы линейный, плотности и времени, все остальные масштабы определяются как:

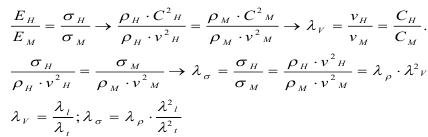
Рассмотрим на примере установление критериев подобия при короткозамедленном взрывании. Здесь необходимо определить период замедлений между рядами скважин в модели, если известны параметры натуры, т.е.:
T - интервал в натуре, с;
ρ - плотность среды, кг/м3;
а - расстояние между скважинами, м;
Cp - скорость продольной волны, м/с;
σ - напряжение на фронте волны, кг/м2;
g - ускорение силы тяжести, м/с2.
Независимыми размерностями являются Т(с), a=L( м), m(М) кг, все остальные - зависимые.
Время T от этих параметров находится в зависимости:

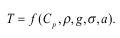
Данная функция может быть и степенным одночленом типа:

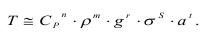
Представим размерности параметров одночлена:

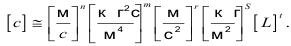
Размерности обеих частей уравнения должны быть одинаковыми, а это возможно, если степени при одинаковых размерностях будут равны, тогда получим систему уравнений:

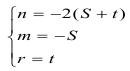
Решим системы у относительно n, m, r; тогда получим:

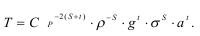
Отсюда находим три критерия подобия:

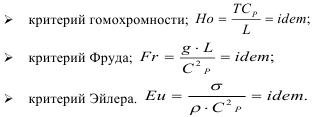
Теперь определим условия выполнения подобия. По критерию гомохромности получим:

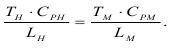
Поскольку нас интересует период замедления, то он в модели должен составлять:

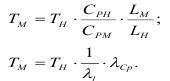
Соблюдение условий кинематического подобия, т.е. моделирование перемещений по критерию Фруда обязывает выполнить следующие условия:

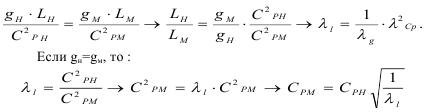
Из последнего следует, что время протекания процесса перемещения при равенстве ускорения силы тяжести в модели и в натуре, будет равно:

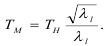
В случае, когда моделирование проводится в центрифуге или на механическом линейном ускорителе при gм=gн*λн, время протекания процесса в натуре и модели равны Tм=Tн.
Как следует из изложенного выше, выполнить все эти условия очень трудно при заданном геометрическом масштабе, особенно условия gм=gн*λн.
по которому необходимо увеличить ускорение силы тяжести на модели в А, раз. He меньшие трудности возникают и по критерию Эйлера, который требует равенства скоростей упругих волн в материале модели и натуры, т.е. по существу это должен быть один и тот же материал. Ho даже в таком случае массив и образец (модель) далеко не одно и то же вследствие масштабного эффекта.

---