Скачкообразное поведение напряженно-деформированного состояния твердых тел

Результатом взрывного нагружения массива горных пород является развитие хаотичных структур в виде трещин во взорванном материале. При взрыве зарядов сферической или удлиненной формы только в ближней и средней зоне в пределах 10d3 наблюдается сеть трещин более или менее закономерно распределенная в объеме в виде радиальных и тангенциальных трещин, за пределами этой зоны все более проявляется хаотичный характер распределения трещин, что хорошо согласуется с концепцией фрактальности.
Термин «фрактал», т.е. дробный, отражает изломанный, фрагментарный характер объектов и явлений с дробными размерностями, являющимися количественной мерой негладкости фракталов.
Концепция фрактальности выделяет объекты и явления, в основе которых лежит гипотеза самоподобия или скейлинга. В качестве фрактальных структур можно рассматривать, например, линии берегов, рельеф местности, турбулентные потоки, организации живых систем, странные аттракторы в фазовом пространстве динамических систем с хаотическим поведением, структуры месторождений, дисперсные системы и т.п. образования.

Основным свойством фракталов является нецелое значение их размерностей. Для характеристики фрактальных множеств имеется две группы определения типа размерности:
- характеристики меры, полученные из чисто геометрических соображений;
- характеристики, связанные с теорией информации.
Понятие фрактальной меры и фрактальной размерности множеств базируется на определениях, введенных Хаусдорфом и Безековичем.
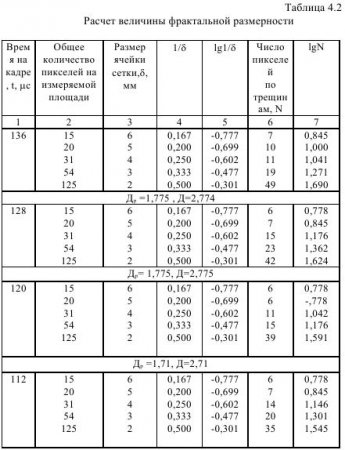
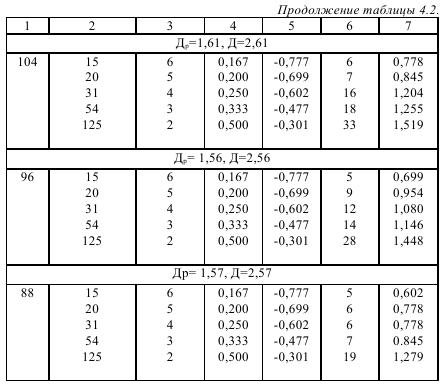
В нашем эксперименте, когда модель не расчленялась на отдельности, а была покрыта сетью трещин, которые определяют размер отдельностей, использована методика определения фрактальной размерности, предложенная М.Ю. Яблоковым, которая состоит в следующем.
На черно-белое изображение накладывается сетка с квадратной ячейкой размером δ. Определяется зависимость количества ячеек N, занятых черными или белыми пикселами, от размера ячейки. Сетчатая фрактальная размерность Др определяется по наклону линии, полученной построением зависимости:

В соответствии с правилами Б. Мандельброта для нерегулярных фракталов фрактальная размерность больше размерности, вычисленной по методу сетки на 1:

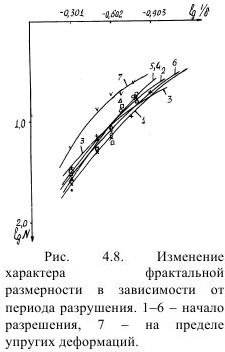
С использованием метода сеток для нашего эксперимента определена сеточная фрактальная размерность Др и затем действительная фрактальная размерность разрушенной (покрытой трещинами) пластины Д. Для измерений и вычислений отобраны фотоотпечатки развития процесса трещинообразования следовавшими по времени через 8 μс. Результаты сведены в табл. 4.2. По данным табл. 4.2 построены кривые в координатах lgN и lgl/δ (рис. 4.8). Большинство кривых образует семейства, которые аппроксимируются уравнением вида:

например, для периода времени 136 μс от начала взрыва, кривая выражается:

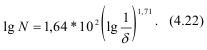
Расчеты позволили впервые выявить закономерность изменения фрактальной размерности по времени процесса (рис. 4.9). Она заметно растет в ходе расчленения пластины из оргстекла трещинами, однако, как и следовало ожидать, при объемном разрушении размерность стала расти, поскольку раскрывались дефекты более низкого порядка.

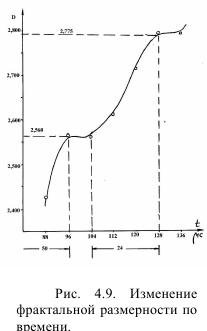
Изменение фрактальной размерности во времени свидетельствует о том, что в процессе должна сформироваться определенная структура разрушения, требующая затрат времени, то есть времени экспозиции энергии и разрушающего напряжения.

Сама форма графика (рис 4.9) показывает, что процесс разрушения также имеет скачкообразный характер, отчетливо видны в данном случае (в пределах времени съемки) два периода, между которыми скачек процесса разрушения происходит в виде «цепной реакции». Это подтверждается анализом продолжительности времени до первой горизонтальной площадки изменения фрактальной размерности (рис 4.9), которое составило около 56 μс, в то время как до второго прошло всего около 24 μс.
Вполне возможно, что при увеличении удельного расхода BB и повышении скорости съемки, удалось бы выявить более двух периодов (скачков) изменения фрактальной размерности.
Таким образом, имеем самоускоряющийся и самоподдерживающийся процесс разрушения, что характерно для таких явлений, как горный удар. Аналогией может служить также диэлектрический пробой в горной породе, когда вероятность возникновения и роста пробоя P(E) зависит от напряженности электрического поля E3 на поверхности: P(E) =En и при этом фрактальная размерность Дпр меняется непрерывно с изменением n.
Подобной модели разрушения при диэлектрическом пробое являются модели материалов, построенные на накоплении напряжений (σ), когда им пропорциональна вероятность разрушения (F(x)):

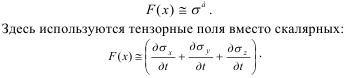
Эта Виттен-Сендоровская модель свидетельствует, что в кластере трещин под действием напряжений σх,у,z некоторое время «изучаются» все возможные соединения трещин, a затем выбирается одно случайное и не обязательно большее значение σ, в том числе не обязательно в данном направлении.
Выявленные выше закономерности также подтверждаются экспериментально доказанным изменением величин относительных деформаций тыльной стенки скважины на модели.
Если условно считать, что пластина оргстекла, вырезанная в виде уступа, находится в механически равновесном состоянии, то после того как она будет подвержена взрывному нагружению, начнет происходить обмен энергией между неоднородностями (структурными элементами) и часть ее будет диссипирована. Рост трещин, их пересечение, формирование отдельностей уже после взрывчатого разложения заряда BB означает, что отдельности не могут более обмениваться энергией с соседними частями.
Поскольку величина заряда была подобрана так, что модель уступа после взрыва не рассыпалась, а только покрывалась трещинами различной интенсивности, что придало пластине характер блочного строения, то трещины, будучи результатом разрушения, являются также способом существования пластины при больших предельных необратимых деформациях.
Именно это положение нами теоретически и экспериментально доказано и в данном случае подтверждено, что в ближней зоне взрыва, в области пластического течения, в пределах 5dз, примыкающей к зарядной полости, образуются более мелкие фракции. Они препятствуют росту более крупных, вследствие диссипирования большей доли энергии взрыва. Данный факт также подтверждается и ростом фрактальной размерности во времени, следовательно, ростом многоуровневой структуры разрушения, когда одно- временно происходит: затухание трещин, выход их на свободные поверхности соседних отдельностей, увеличение их протяженности.
Величина фрактальной размерности, характеризующая степень сложности структуры, очевидно, возрастает с увеличением вновь образованной поверхности. Выявленные горизонтальные площадки на графике изменения во времени величины фрактальной размерности свидетельствуют, что процесс разрушения идет через последовательное избирательное укрупнение кусков от положения заряда и уменьшение их количества. При этом можно выделить следующие элементы эволюции структуры разрушения по зонам:
- в ближней - мельчайшие обломки изометрической формы;
- в средней - сложно построенные отдельности, вытянутые в направлении действия главных напряжений;
- в дальней - магистральные трещины сложной конфигурации.
В целом напряженно-деформированное твердое тело может рассматриваться как многоуровневая самоорганизующаяся структура, эволюция которой под нагрузками представляет собой характерный синергетический процесс.
Анализ характера изменения величины фрактальной размерности во времени показал явную стадийность развития процесса деструкции. Поведение фрактальной размерности «Д» показывает, что каждую из выделенных стадий деструкции можно рассматривать как определенный иерархический структурный уровень с определенным комплектом структурных элементов и соответствующим ему механизмом деформации.

---