Дилатонный механизм разрушения твердых тел

Наиболее ранее использование термина дилатон относится к 1978-1979 гг., который был применен А.А. Кусовым, а затем С.Н. Журковым, В.А. Петровым и др. Дилатоном называют отрицательные флуктуации плотности. Дилатон можно определить иначе - как область растяжения пониженной плотности. Первое определение означает, что еще до разрушения и образования любой величины дефекта в образце образуется повышение плотности к краям и снижение ее в центре (рис. 1.16). В такой интерпретации определения тождественны. В этом случае дилатон - это нематериализованный дефект или виртуальный дефект размером λ и продолжительностью жизни τd.

Чтобы понять основные отличия дилатонного механизма прочности от известных, укажем на них. По современным представлениям разрушение твердых тел включает взаимосвязанные процессы: возникновение зародышевых трещин и накопление около них концентраторов напряжений выше критических. В объяснении дилатонного механизма разрушения важно выяснить причину возникновения колебаний плотности. Эти колебания возникают спонтанно, вследствие хаотичного движения атомов или же в результате суперпозиции упругих волн.
Размер области флуктуации плотности определяется длиной свободного пробега фононов λ. Линейный размер λ зависит от неоднородностей твердого тела, а применительно к мало дефектным телам эта неоднородность определяется сменой температур.
Время жизни флуктуации и, следовательно, дилатона равна:

где Cp - скорость звука.
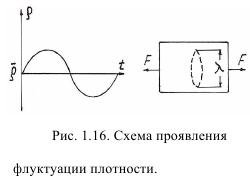
Судя по рис. 1.16 дилатон возникает при растяжении, при сжатии этого не происходит, поскольку края сдвигаются. Внутри дилатона все межатомные связи растянуты (деформированы) на величину:

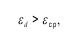
где εd и εср - деформации связи в дилатоне εd в сравнении со средней деформацией материала εср.
Благодаря последнему неравенству плотность дилатона меньше средней плотности материала и тогда он становится ловушкой для фононов, которая может накапливать энергию фононов. Накачка энергии приводит к разогреву дилатона, последующему расширению его до критической величины и распаду.
Роль дилатона в этом распаде и разрушении вытекает из анализа кинетического уравнения прочности С.Н. Журкова:

где τ - долговечность материала, т.е. время от нагружения до распада (длительность испытания);
τ0 - период тепловых колебаний атома, примерно 10-13 с;
γ - активационный объем;
σp - растягивающее напряжение;
к - постоянная Больцмана;
T - абсолютная температура;
U0 - энергия межатомных связей.
Решая последнее уравнение, определим уровень растягивающих напряжений при заданной длительности испытания:

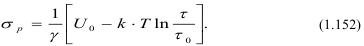
Это уравнение можно преобразовать через модуль упругости в сочетании с линейным коэффициентом расширения:

где ε≈0,2 деформация разрушения, является предельной величиной деформации межатомных связей, при которой связь теряется и тело распадается; % - коэффициент перегрузки.
Следует еще выразить энергию межатомных связей через предельную деформацию и теплоемкость:

где ca — атомная теплоемкость; α - линейный коэффициент расширения.
Активационный объем также заменяется:

Если положить, что χ=1, т.е. перегрузок нет, то для распада дилатона и образования зародышевой трещины (1.65) перепишется в виде:

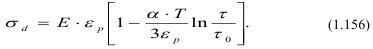
В случае, когда деформация межатомных связей равна:

тогда,

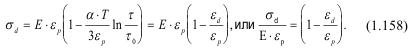
Здесь σd/εP*E - величина безразмерная, как и правая сторона уравнения (1.158).

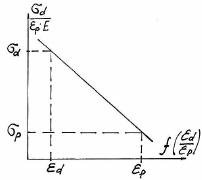
График σd/εp*E=f(εd/εp) представлен на рис. 1.17.

Деформация εd - есть удлинение дилатона при растяжении твердого тела, при достижении критического значения накачка энергии становится обратимой, а отношение:

где а - атомный размер; λ - длина свободного пробега фонона, т.е.

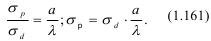
Подставляя (1.161) в (1.158), имеем:

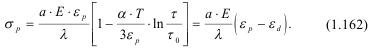
Сравнивая (1.162) и (1.153), обнаружим, что механический концентратор χ имеет смысл:

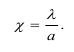
Уравнение (1.162) показывает, что в твердом теле дилатоны возникают спонтанно, они имеют размер λ, а деформация составляет εd.
Как указывалось ранее, накачка энергии приводит к росту деформации εd, достигнув предела, дилатон распадается, образуя зародышевую трещину.
Сам распад дилатона происходит с огромной скоростью, т.е. его жизнь по времени составляет:

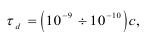
что равно: τd=λ/Cp.
Вероятно, тd для различных материалов остается почти постоянным, тогда при известной скорости Cp можно определить длину пробега фонона:

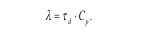
Например, для оргстекла, имеющего Ср=2100 м/с, λ составит 0,0021 мм. Если при этом время распада равно 10в-9 с, то сам распад равнозначен микровзрыву с временем действия ударной волны в 1 не, с которым в действительности не детонирует никакое известное в настоящее время ВВ.
Взрывоподобный механизм, обусловленный распадом межатомных связей в дилатоне сопровождается звуковой, световой и электрической эмиссиями, что наблюдается при разрушении твердого тела.
Из (1.162) следует, что длина свободного пробега фонона обратно пропорциональна прочности и, наоборот, для прочных твердых тел должен быть малым путь пробега. Аппроксимация данных С.И. Журкова для металлов, дает следующие соотношения:

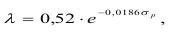
или

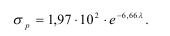
Подобная зависимость прочности от длины свободного пробега фонона определяется структурной неоднородностью твердых тел.
При взрыве на границе области дилатона возникает скачок давления и тогда сам дилатон является не только очагом локальной области разрушения, но и одновременно точечным флуктуационным источником дислокаций.
Дилатонный характер разрушения твердых тел вносит серьезные поправки в трактовку механизма разрушения по теории Гриффитса, когда основой ее считается наличие дефектов в твердом теле и, следовательно, должна быть определенная последовательность во времени возникновения пластических и упругих деформаций. Дилатонный механизм объясняет взаимосвязанность пластической деформации с самим разрушением.
Как известно, синергетический процесс характеризуется наличием открытой нелинейной системы, обеспеченной возможностью обмена энергией с окружающей средой.
Если через дилатон идет поток тепловой энергии в виде фононов, то, как утверждает В.А. Петров, это вызовет изменение неравновесной объемной плотности энергии Ev.
Уравнение кинетического баланса выглядит как:

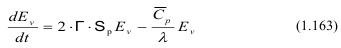
где Г - коэффициент поглощения.
Если предположить условие равновесия в дилатоне (рис. 1.16, правая часть), то это значит, что прирост деформации ε обеспечивается термодинамическим соотношением:

где к - сжимаемость среды;
G - термодинамический коэффициент Грюнайзена Q, равный:

где V - объем.
Так как р должно уменьшаться при T=Const, то перед 1/V стоит знак минус, чтобы G был положительным.
В уравнении (1.163) Г - коэффициент поглощения равен:

где ε - деформация; а - межатомное расстояние.
Если подставить в уравнение (1.162) значения всех входящих в него составляющих, то получим кинетическое уравнение для деформации е межатомных связей в дилатоне:

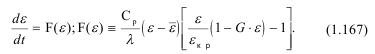
В (1.167) ε - равновесная деформация, а прирост деформации равен:

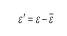
Критическая деформация составит:

В (1.167) F(ε) - есть полином, корни которого дают решение (1.167) (рис 1.18):

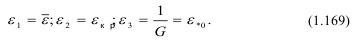
Эти корни являются точками уравнения (1.167), а по сути являются стационарными состояниями дилатона.
Если продифференцировать (1.167), то можно получить положение точек на оси:

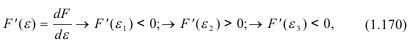
где при ε1, ε2 и ε3 - соответственно отмечаются устойчивость, неустойчивость и стремление ε к критическому значению и вновь устойчивость.

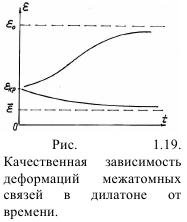
Решение уравнения (1.167) относительно εкр выглядит, как показано на рис. 1.19, соответствующее корням, а εкр является точкой бифуркации. Значения ветвей зависят от положения ε в начальный момент времени.
Возможны две ветви:
- εεкр - деформация растет, обеспечивая устойчивое стационарное состояние,
при ε0= 1/G происходит разрыв межатомных связей, т.е. образуется стабильная зародышевая трещина.

В стационарном состоянии вытекающие и втекающие потоки энергии через дилатон равны, значит, поток энтропии через дилатон при температуре Tx соответствует:

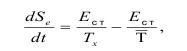
т.е. дилатон отдает энтропию.
Уменьшение энтропии приводит к самоорганизации твердого тела в дилатоне и обеспечивает переход в новое устойчивое структурное состояние, обладающее меньшим числом степеней свободы, называемое по терминологии И. Пригожина диссипативным. Сама трещина является диссипативной структурой, она возникает в неравновесной открытой нелинейной системе вдали от положения равновесия скачкообразно при критическом значении параметров, переходящих через точку бифуркации.
В дилатонной модели механизм зарождения трещин является собственным, т.е. он возможен в бездефектном теле, и этим отличается от подхода Гриффитса. Однако насколько отличается? Для Гриффитса дефект — это несполшная структура твердого тела, для дилатонного механизма - это структурные дефекты плотности, в окрестностях которых стартовая деформация ε- повышена, и в данном случае структурные дефекты плотности вызывают структурные привязки трещин.

---