Влияние скорости деформации на результаты разрушения

Характер роста трещин, как процесс быстро протекающий, лучше наблюдать на моделях. В работе В.И. Родионова материалом модели служила канифоль, которая при определенных температурах разрушается хрупко, кроме того, она полупрозрачна.
Опыты проводились на образцах диаметром 60 мм и высотой 120 мм. Чтобы исключить ускорение деформирования, имелся пластический ограничитель из алюминия, при этом образец оказывался внутри него. Для сдерживания поперечного расширения образца его помещали в обойму из алюминия, тогда можно обойтись без ограничителя сверху.
Деформация регистрировалась по перемещению подвижной плиты индикатором часового типа. Образец имел параметры: ρ=1,08 г/см3, Ср=2,37 км/с, Cs=1,04 км/с.
При скорости деформации 5*10в-6 1/с первые трещины появлялись при деформациях 0,01-0,02 и вместе с этим начиналось шелушение образца, т.е. отслоение чешуек до 1 мм и толщиной 0,1 мм. Полное разрушение наступало при достижении 10-15% деформации. Эти опытные данные позволяют оценить некоторые параметры разрушения.
1. Время нагружения до начала разрушения, т.е. до появления первых трещин. Они появились при деформации Uxx=0,01-0,02, в среднем Uxx=0,015=1,5*10в-2. В этом случае время деформации составит:

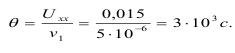
2. Напряжение растяжения на берегах трещины:

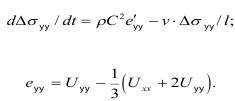
При v=const, имеем:

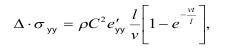
при t→0, имеем:

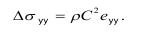
Девиаторная деформация еуу (сумма деформаций по большим диагоналям ∑e=0) может быть выражена через осевую Uxx при известной связи Uyy=-vUxx:

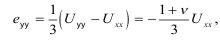
где еуу - характеризует деформации сдвига. Напряжения выражаются как:

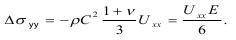
Для данного испытания, когда Е=3*10в3 МПа оно равно:

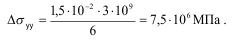
Минимальный размер неоднородности составит:

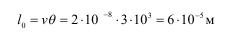
при скорости релаксации напряжений V= 2*10в-8 м/с.
Если добротность Qm - есть показатель концентрации напряженностей в теле, то так как образец канифоли выплавлялся, то у него таких неоднородностей было немного, т.е. Qm была велика и имела порядок 10в3, (например, в нижней мантии Земли она примерно равна 2*10в3). Тогда, согласно сказанному выше, имеем:

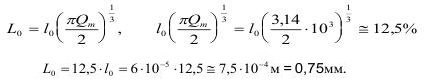
Эта величина почти равна величине чешуек, отскакивающих от боковых поверхностей образца.
При опытах с боковым подпором нагружение образца производили при скоростях деформации 3*10в-6 1/с, назовем ее малая, и 90*10в-6 1/с (большая). Так как скорости отличались в 30 раз, различие в разрушении оценивалось по величине кусков. Разрушенные образцы просеивались через сита с отверстием хi , а результаты представлены в табл. 1.1.

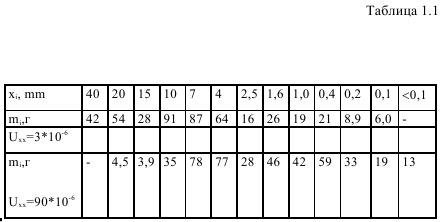
Если воспользоваться законом Вейбулла и построить график в осях lglgm0/m+ и lgx , то можно определить Xm и n для этих двух распределений:

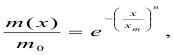
где mх - масса, оставшаяся на сите (обозначим + в сравнении с размером сита), т.е. размером, большим х.
Для малых скоростей получим Xm=13,1 mm и n=1,01, для больших скоростей хm=3,9 и n=0,9. Теперь видно, что расстояния между неоднородностями L0 обратно пропорциональны скорости нагружения.
Изложенное выше относится к механическому разрушению. Сравним эти положения с данными О.Е. Власова и С.А. Смирнова, которые показали, что в процессе разрушения характеристики среды непрерывно меняются, т е. возможны переходы от упругой к пластической модели материала и обратно. Этими авторами доказано, что при приложении сжимающих напряжений возможно лишь пластическое разрушение, но это противоречит работам Г.И. Покровского, Г. Кольского и других, которые доказывают, что при приложении сжимающих напряжений в перпендикулярном направлении, возникают касательные растягивающие напряжения, определяющие появление радиальных трещин.
О.Е. Власов и С.А. Смирнов предполагают, что хрупкое разрушение возможно лишь при обратном движении среды (откольные явления), когда сжимающие напряжения меняют знак. Г. Кольский установил, что при высоких скоростях нагружения даже чисто пластические материалы подвержены хрупкому разрушению, т.е. пластические деформации среды не происходят, а появляются радиальные трещины. В таких материалах хрупкого разрушения не наблюдается, т.к. касательные напряжения релаксируют. Чем выше скорость релаксации, тем более пластичен материал. При высоких скоростях нагружения (например, взрывном) даже в пластических материалах касательные напряжения не успевают релаксировать, поэтому характер разрушения не отличается от хрупкого.
Квазихрупкое разрушение предполагает, что при разрушении значительная доля деформаций приходится на пластику. Тогда возможно решение задачи по определению среднего вероятного куска:

где Vs — критическая скорость, соответствующая пластическим деформациям, м/с; Dдр - критерий дробимости.
Известно, что средний кусок зависит от радиуса заряда, расстояния между зарядами и физико-механических показателей среды, что увязывается в соотношениях:

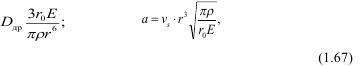
где E — модуль упругости; ρ - плотность породы; r — расстояние от заряда до рассматриваемой точки, м; r0 - радиус заряда.
Из (1.67) следует, что размер куска увеличивается с расстоянием от заряда и уменьшается с ростом радиуса заряда и его энергией, при этом зона дробления составит:

Рассмотрим известное из геомеханики и теории упругости соотношение:

где ρ - плотность, гс2/м4; Cp - скорость продольной волны, м/с; U -скорость смещения (м/с).
Модель твердого тела Максвелла выглядит так:

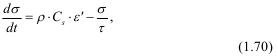
где Cs - скорость поперечной волны сдвига; ε' - скорость деформации, т.е. de/dt.
Исследование размерности (1.69) и (1.70) показывает, что для первого она соответствует г/см2, а для второго - г/см, т.е. усилие распределено по Δσl = ρ*C2s*ε'*t, длине.
Чем больше размер неоднородности, тем выше напряжение при заданной скорости деформации. Если тело велико, то в нем при любой скорости деформации всегда найдутся неоднородности большого размера, на которых избыточное напряжение приведет к разрушению. Если это избыточное напряжение соответствует:

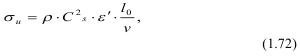
то минимальный размер неоднородности равен:

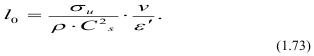
Таким образом, при постоянной скорости деформации среди параметров твердого тела появляется параметр с размерностью длины, и твердое тело утрачивает свое безразличие к масштабу.
Из (1.73) следует, что для всякого твердого тела конечного размера можно подобрать такую низкую скорость деформации, при которой оно не будет разрушаться, т.е. наблюдается явление крипа из-за релаксации напряжений.
При высокой скорости деформации дополнительные неупругие напряжения, складываясь с упругими, приводят к увеличению жесткости тела, а иногда и к увеличению эффективной прочности, но это не является динамической прочностью.

---