Законы дробления

Образование новых поверхностей при дезинтеграции породы процесс достаточно энергоемкий и управляется в соответствии с несколькими законами.
Закон Риттингера (1867 г.) описывает связь затрат энергии и вновь образованной поверхности:

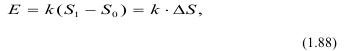
здесь k - некоторый коэффициент пропорциональности, имеющий размерность удельной поверхностной энергоемкости разрушения, МДж/м2.
При дроблении определенного количества породы Q0 от начального куска размером D до конечного d нужно затратить работу:

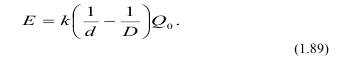
Средние диаметры кусков до и после дробления D и d можно определить как средневзвешенные:

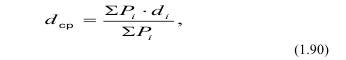
где Pi - весовой выход данного класса крупности, установленный гранулометрическим анализом, %; di - средний диаметр данного класса крупности.
При использовании данного закона Риттингер предполагал, что удельная поверхностная энергоемкость дробления не зависит от величины энергии удара и формы ударяющей поверхности.
В 1874 г. В.Л. Кирпичев, а в 1885 г. Кик предложили гипотезу, согласно которой энергия расходуется на изменение формы геометрически подобных и однородных тел и изменяется пропорционально объемам или массам этих тел:

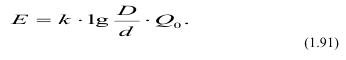
Расход энергии на дробление данной породы зависит только от степени дробления, т.е. D/d и не зависит от крупности дробленого материала.
Законы Риттингера и Кирпичева-Кика аналогичны, если средний диаметр вычислять по логарифмам:

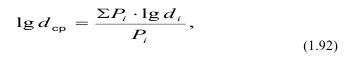
тогда уравнение запишется в виде:

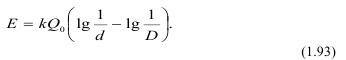
Законы Риттингера и Кирпичева-Кика объединяются обобщенным законом П.А. Ребиндера, согласно которому полная работа дробления состоит из работы деформации в объеме разрушаемого куска ΔV и работы образования новых поверхностей ΔS, т.е.:

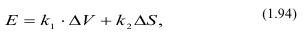
где k1 и k2 - коэффициенты пропорциональности, соответствующие удельной объемной энергоемкости МДж/м3 и удельной поверхностной энергоемкости МДЖ/м2.
По аналогии с этим, А.Ф. Суханов предполагал в формуле для расчета массы заряда BB также использовать два удельных расхода, соответственно идущих на создание поверхности отрыва и на дробление и преодоление силы тяжести:

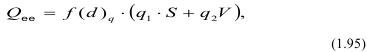
где q1 — удельный расход BB на 1 м2 площади отрыва от массива;
q2 - удельный расход BB на дробление 1 м3 и преодоление силы тяжести;
f(d)q - коэффициент, учитывающий степень дробления.
В предыдущем уравнении полная работа дробления связана с пластическими и упругими объемными деформациями и образованием новых поверхностей.
Законами дробления занимались Ф.С. Бонд и Р. Чарльз высказали предположение, что полная работа разрушения обратно пропорциональна квадратному корню из диаметра кусков:

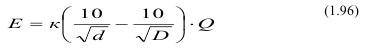
а затем ввел понятие «индекс работы» - по существу удельную энергоемкость дробления.
Позже закон Бонда был преобразован к виду:

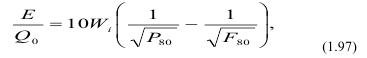
где E - энергия дробления;
Q0 - масса дробленного продукта, г;
Wi - индекс работы, МДж/г;
P80 и F80 - размер соответственно выходного и входного отверстий через которые проходят 80% материала.
Многочисленные опыты на 51 виде образцов дали следующие значения Wi - 44 МДЖ/т или 13,8 кВтч/т. Эта величина нам потребуется в дальнейшем при сравнении ее с удельный энергоемкостью при бурении.
В 1957 г. Р. Чарльз предложил выражать затраты энергии в зависимости от уменьшения линейного размера разрушаемого материала:

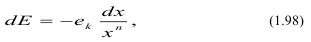
где dE - работа, затраченная для изменения размера исходного куска х на величину dx; ek - удельная энергоемкость разрушения.
Интегрирование уравнения в пределах d и D при учете показателя степени дробления n=2 дает:

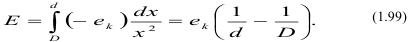
Это соответствует закону Риттингера. При n=1 соответствует закону Кирпичева-Кика:

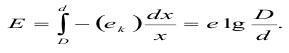
При n=1,5 - превращается в закон Бонда

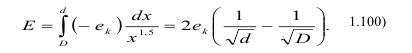
Итак, получены близкие, но все же различные зависимости, ходя все описывают одинаковые процессы разрушения. По существу, значения показателя степени n — есть выражение масштабного эффекта. При крупном дроблении (закон Кирпичева-Кика) размеры дефектов и микротрещин малы в сравнении с размерами кусков материала. В области более тонкого измельчения, когда размеры дефектов соизмеримы с размерами частиц, а их количество в разрушенном объеме относительно мало, поэтому раскрытие новых поверхностей может идти с включением дефектов более низкого порядка. Таким образом, разница в показателях степени дробления определяется структурой неоднородностей пород и масштабами самого процесса.
Известные гипотезы и теории разрушения рассматривают предельные величины напряжений, а как известно, их определение затруднено, и тем более трудно определить совместное разрушающее воздействие от напряжений различного вида.
В законах дробления Риттингера, Кирпичева-Кика и Бонда все уравнения с одним неизвестным в виде коэффициента пропорциональности «к» или «ек», - выступающего в качестве удельной энергоемкости разрушения и легко определяемого конечного результата в виде вновь образованной поверхности. Коэффициенты пропорциональности идентичны и равны:

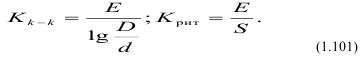
Задача установления пределов использования и оценки результатов гранулометрического анализа, довольно простой операции, сводится к вычислению средних диаметров частиц Dcp и dcp и зависит от их вновь образованной поверхности Sн, которую можно определить как:

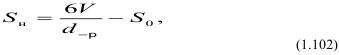
где V - объем разрушенной породы, м3; S0 - площадь поверхности до разрушения.
Применимость последней формулы ограничивается степенью дробления. При высокой степени дробления возможны большие погрешности по причине ошибок при задании границ классов. Для более точного определения используют уравнение Розина-Раммлера:

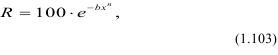
где R - суммарный выход класса, крупнее х по плюсу, %; х - размер отверстий сита; b и n - параметры, зависящие от свойств материала и размерности х, а n - как показатель, характеризует рассеяние частиц по крупности, чем больше n - тем выше однородность материала.
После выполнения гранулометрического анализа соответствие опыта уравнению можно проверить графически, построив кривую распределения в координатах: lgx и lglg(100/R). Координатные оси получаются в виде:

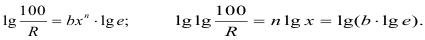
В указанной системе координат уравнение (1.103) есть прямая с угловым коэффициентом n.
В случае, если число выделенных классов крупности значительное, например, три и более, и особенно при наличии мелких фракций, а именно они дают наибольшую новую поверхность, величину вновь образованной поверхности Sн следует определять не по среднему диаметру фракции (dcp), а в виде суммы

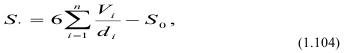
где Vi, di — соответственно выход данного класса крупности и его диаметр.
В последнем уравнении первое слагаемое в виде суммы может принимать гигантские значения, так как все здесь зависит от dcp, и чем он меньше, тем значительнее сумма. Следовательно, все зависит от выделенных классов и если доля малых фракций больше, то и Sн может оказаться намного больше, чем рассчитанная по формуле. Именно по этой причине коэффициенты пропорциональности в законах Риттингера и Кирпичева-Кика искажаются.
Законы разрушения Риттингера, Кирпичева-Кика и Бонда установлены при использовании положения о квазихрупком разрушении, основой которого является допущение, что константой материала является поверхностная энергия. Это допущение не противоречит механизму разрушения твердых тел, особенно ограниченного размера, когда их можно условно рассматривать как бездефектные. Тогда и проявляется постоянство поверхностной энергоемкости разрушения.
Физические процессы горного производства имеют дело с различными уровнями объектов разрушения, а также с различными уровнями дефектности и плотности (количеством) этих дефектов, да и характер их разный. Поэтому механизм разрушения различается, в том числе и его результаты. Затраты энергии на образование единицы площади вновь образованной поверхности зависят от данного уровня разрушения.
Для объяснения этого явления лучше всего рассматривать взрывное разрушение последовательно от ближней зоны к дальней. В ближней зоне величиной (2-4)r разрушение происходит за счет преодоления энергии связей между молекулами, далее, на расстояниях (3-8)r - преодоление связей между кристаллами или минералами, и в дальней, за пределами (5-10)d, по микро- и макродефектам. Еще дальше в зоне (10-30)d - преодоление сил сцепления.
Аналогично, при дроблении пород в дробилках и мельницах также различают стадии крупного от 1500-300 до 300-100 мм, среднего от 350-100 до 100-40 мм и мелкого дробления от 100-40 до 80-5 мм. Вероятно, количество дефектов с ростом диаметров кусков должно расти в di3 степени.
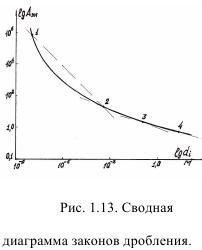
Если на графике отложить энергоемкость Аэн разрушения (кВтч/т) породы, а на оси абсцисс - крупность продукта в логарифмическом масштабе, то на кривой можно выделить 3 участка соответствующие трем законам разрушения (рис. 1.13). На участке 1-2 проявляется закон Риттингера, на участке 2-3 - закон Бонда и на участке 3-4 - закон Кирпичева-Кика. При этом искажение коэффициентов пропорциональности «к» больше на первом участке мелкого дробления, и оно незначительно на последнем участке, практически совпадающем с направлением оси абсцисс.

---