Структура разрушения горных пород

Под разрушением обычно понимается распад твердого тела на не связанные между собой отдельности. В инженерной практике встречаются два случая разрушения: разрушение безграничного пространства и разрушение тел ограниченных размеров. Если в первом случае результат непредсказуем, то во втором — предсказать результат можно и при этом геометрия тела и уровень напряжений будут играть главную роль.
Растягивая стержень с небольшой скоростью, во избежание проявления сил инерции, можно установить, что по достижении определенной величины, растягивающие напряжения разорвут стержень точно в одном месте.
Распределение напряжений по длине стержня равномерное, т.е. они одинаковы, но разрыв наступает только в одном месте и это место непредсказуемо. Ясно, что в месте разрыва существовал дефект, но знать эти места - задача невыполнимая, поскольку местоположение точки равновероятно по всей длине стержня, хотя возможно предположение о числе таких мест ослабления. Например, в эксперименте А.Н. Ханукаева, когда при взрывании на торце стержня из оргстекла от его свободного конца отрывалось N кусков, чему способствовало соотношение:

где σz - максимальное растягивающее напряжение, зависящее от массы заряда и уменьшающееся от центра заряда с расстоянием; [σ] -предел прочности материала на разрыв.
Вероятная длина каждого куска может быть установлена по формуле:

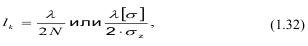
где λ - длина волны, зависящая от Т - периода и амплитуды колебаний.
Если считать верным, что [σ] отрыва меньше любых других напряжений, то волна напряжений должна пройти путь:

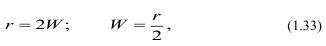
где W - линия наименьшего сопротивления.
Для относительно монолитного образца от его торца оторвется 1 кусок равный W. Задаваясь размером кондиционного куска 1, например, по ширине ковша экскаватора, найдем:

Чтобы получить подобный результат, нужно, чтобы напряжение было равно:

Следовательно, распределение мест ослаблений по длине стержня - явление случайное. Задачу можно поставить иначе: какое количество слабых мест имеется на длине стержня в момент разрушения, а мерой слабости является отклонение от средних напряжений, разрушающих стержень. Для расчета параметров разрушения В.И. Родионов, В.М. Цветков и А.И. Сизов рекомендуют следующие основные зависимости.
1. Развиваемое напряжение растяжения при малом времени воздействия:

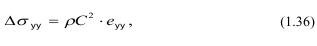
где ρ - плотность материала; С - скорость продольной волны в материале; еуу - деформация сдвига.
2. Деформация сдвига, соответствующая девиаторной (сумма диагональных элементов) составляющей и связанная с осевой деформацией Uxx:

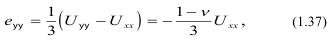
где Uyy Uxx - деформации по осям; v - коэффициент Пуассона.

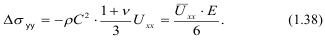
где Uxx - средняя деформация.
3. Минимальный размер неоднородности при данном напряжении:

4. Расстояние между неоднородностями, находящимися под напряжением:

В такой постановке количество слабых мест разной меры слабости на длине стержня, определяет статистический разброс показателя прочности. Очевидно все дело в структуре твердого тела.
В.И. Родионовым модель твердого тела представляется с неоднородностями, на которых при постоянной скорости нагружения возникает свое избыточное над средним напряжение, зависящее от размера неоднородности.

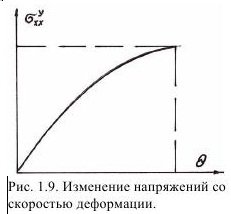
При постоянной скорости деформации упругое напряжение σy xx возрастает со временем θ, (рис. 1.9) до момента разрушения. Это время позволяет разделить неоднородности на две группы:
1) на мелких неоднородностях с размерами ll0.
Концентрация предельных напряженных неоднородностей в объеме, где L>>l0, фактически определено концентрацией (количеством) неоднородностей размером l0, т.е.:

Откуда:

Здесь n0 - число неоднородностей в единице объема, тогда пространство, приходящееся на одну неоднородность размером l0 равно:

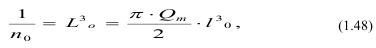
или

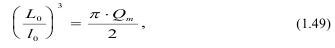
где L30 - объем пространства.
Если сечение стержня S=L20, то расстояние между неоднородностями по длине стержня будет в среднем равно L0:

Из (1.50) следует, что чем больше добротность Qm, тем меньше число неоднородностей.
Рассмотрим два случая применительно к сечению стержня:
а) диаметр стержня много меньше l0, тогда избыточное напряжение по сравнению со средним напряжением мало, так как θV=l0>>d:

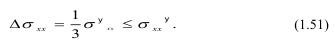
В этом случае структура неоднородности не может себя проявить, а сам случай является примером медленного деформирования, когда напряжения на неоднородностях не успевают релаксировать. При низкой добротности Qm и больших размерах тела, возможно течение тела при напряжениях ниже средних (явление крипа);
б) диаметр стержня много больше размера неоднородности, т.е. d>>l0 или при большой скорости деформации, в этом случае:

Разрушение тела обусловлено тем, что на неоднородностях напряжения достигли предела прочности:

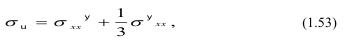
- если концентрация неоднородностей мала, а добротность Qm велика, то неупругие напряжения малы и стремятся к 0 и, следовательно:

- если концентрация неоднородностей велика, и Qm - мало, при быстром нагружении работают все неоднородности от lo и до d, то суммарное напряжение σхх будет приближаться по величине к напряжению на неоднородности σu.
Отсюда следует, что при увеличении скорости нагружения возникает представление об увеличении предела прочности. На самом деле причина заключается в кинетике разрушения тела, а именно, связана с его структурой.
Рассмотрение структур напряженных неоднородностей на стадии подготовки разрушения показывает, что при заданной скорости нагружения происходит выделение неоднородностей одного размера. Отмеченное выше позволяет сделать вывод: «Каждой скорости нагружения соответствуют неоднородности своего размера, т.е. при деформировании тела наступает упорядочение структуры в смысле распределения неоднородностей по размерам».
Для описания распределения размеров кусков при дроблении используется много законов, в том числе Розина-Раммлера и Вейбулла:

где V/V0 - часть объема, раздробленного на куски более X; Xm и n-параметры распределения.
В дифференциальной форме (1.55) может быть представлено в виде:

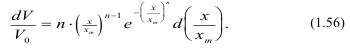
Знак минус опущен, так как он не имеет значения, речь идет об убывании мелочи или крупных кусков, т.е. dV или d(V0-V). Если заменить объем количеством, т.е. dV/V на x3dN, то при n=1 получим:

Для мелких фракций (х<<хm) получим выражение еще проще:

При отсутствии у твердого тела структуры, минимальный размер частиц ничем не ограничен (вплоть до размера атома), т.е. на образование мелочи расходуется львиная доля энергии. При отсутствии ограничения в размерах частиц энергия дробления должна возрастать до бесконечности, что противоречит закону сохранения энергии.
Поскольку в твердом теле со структурой имеют место соотношения (1.58) и (1.59), то при неоднородности размером l0 и их равномерном распределении в теле, на каждую из них приходится объем, равный L30=l/n, а расстояние между ними равно L0. На этих расстояниях и начнется разрушение.
Введением минимального куска путем умножения обеих частей (1.58) на L0 можно получить:

После рассеивания дробленой массы по величине L0, (1.59) предстанет при Xi=iL0, (i=l,2,...) в виде:

В (1.60) правая часть представляет собой объем фракций, а левая - вероятность образования кусков разного размера, причем она одинакова, значит L0/xm является вероятностью образования кусков размером L30 Обратная величина вероятности означает количество фракций в результате разрушения:

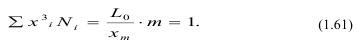
откуда: xm/L0=m - число фракций.
Если разрушаемый объем небольшой, возможно непредставительное распределение фракций, и для того, чтобы оно было представительным, объем максимального куска должен быть равен x3m=(mL0)3. Следовательно, все фракции должны быть объемом не меньше, чем

При числе фракций m необходимый объем образца для определения гранулометрического состава должен быть равен:

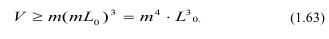
Поскольку l0 и L0 зависят от скорости нагружения, то объем испытуемого образца нужно изменять в зависимости от скорости деформации в соответствии с (1.63).
Процесс разрушения можно трактовать как процесс разрастания трещин до их взаимного смыкания или пересечения, если считать, что на каждой неоднородности l0 зарождается одна трещина, случайным образом ориентированная в пространстве. Связь между крупными и мелкими отдельностями, полученными при разрушении очевидна: крупная отдельность образуется в той части тела, где не смогли сформироваться мелкие. Значит, отдельности формируются в определенном порядке - от мелких к крупным. При этом мелкие отдельности образуются чаще (с большей вероятностью), чем крупные, т.е. они как бы мешают образованию крупных неоднородностей.

Из (1.63) следует, что структура тела имеет отдельность минимального размера L0 и вероятность дробления на куски одного размера составит l/m=Lo/xmax.
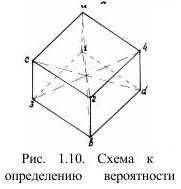
Оценим вероятность образования отдельности минимального размера. Если условно отдельность имеет форму куба (рис. 1.10), то любая трещина располагается в одной из трех взаимно перпендикулярных плоскостей. Трещины будут исходить из всех углов напряженности. Например, из точки 3 могут исходить трещины плоскостей ЗС2В, С3А1, 31ДВ, но вероятность того, что они будут полезными, в смысле отделения куска, составит 1/3. Значит образование четырех граней возможно с вероятностью:

следовательно, вероятность образования каждой фракции одинакова и составит:

Понятно, что цифра 81 получена условно, ее происхождение, как 3в4 показывает путь решения задачи.

---