Теории разрушения горных пород

Прочность горных пород определяется величиной критических напряжений, при достижении которых она разрушается. Уровень напряжений для разных горных пород различный и он является пределом прочности на соответствующие нагрузки (сжатие, растяжение и сдвиг).
Разрушение как факт является понятием, относящимся к процессу, когда происходит разрыв связей между частицами кристаллической решетки. Существует различие в уровнях прочности у моно- и полиминеральных пород.
Наличие дефектов, мелких трещин, их зародышей, неоднородностей состава и состояния, а также плоскостей ослабления - определяет преобладание так называемого хрупкого разрушения. Поэтому для горных пород применима теория хрупкого разрушения Гриффитса.
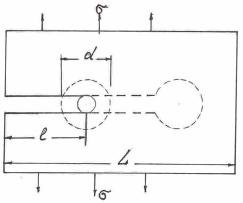
По этой теории (гипотезе) начало разрушения обусловлено наличием некоторой критической трещины (рис. 1.4) в объеме твердого тела.

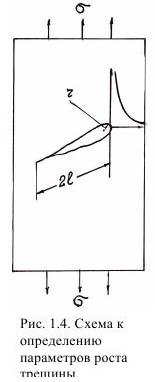
На краях трещины возникает концентрация напряжений, значительно превышающих приложенную нагрузку σ. При длине трещины 2l и радиусе ее закругления r, внутреннее напряжение σ1 равно:

Рост трещин обусловлен выполнением работы Аs, которая пропорциональна удельной поверхностной энергии тела es:

где 4l - две поверхности трещины в пределах толщины тела; es — удельная поверхностная энергия.
В начальной точке роста трещины напряжения снижаются и перераспределяются на другие точки, аналогично структурному дереву Кейли, где снова возникают микросдвиги. Нарастание описанного процесса приводит к разрушению породы. Допуская перераспределение напряжений, можно допустить и возможность перетекания энергии, причем разрушение может наступить даже при некотором снижении ее величины, как будет показано ниже.
Действия внешней нагрузки для образования трещины достаточно, если оно сопоставимо с упругой энергией:

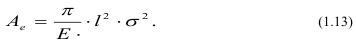
Трещина будет расти, если Ae > As, т.е.

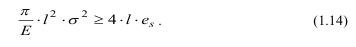
В этом случае критическое положение трещины характеризуется равенством:

откуда:

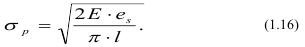
Рассмотренный механизм разрушения может развиваться только при условии хрупкого разрушения. При пластическом разрушении атомы кристаллической решетки скользят с одного уровня на другой, поэтому при разрушении тела требуются меньшие усилия, чем первоначальные. Такое скольжение, однако, возможно в пределах, когда дислокации (дефекты) не выходят на поверхность тела или за границы зерен, имеющих эти дислокации. Как только они касаются поверхности (границ), то уже не принимают участия в пластической деформации.
В отношении приведенных выше рассуждений о неоднородностях, это означает следующее. Если в теле было К дислокаций, при величине неоднородности I0, при расстоянии между ними L0, их число будет уменьшаться, т.е. плотность дислокаций будет также уменьшаться, что приведет к затуханию пластических деформаций и дальнейшее разрушение станет возможным только с приложением дополнительной нагрузки.
На самом деле разрушение даже хрупких пород недостаточно точно описывается теорией Гриффитса, так как кроме концентрации напряжений у вершины трещины, должны быть и пластические деформации в той же вершине. Эти деформации затухают при достижении трещины пределов тела.
Участие в разрушении горных пород как хрупких, так и пластических деформаций способствовало развитию теории квазихрупкого разрушения. Она формулируется следующим образом.
Величина необратимой работы es, затраченной на образование единицы площади свободной поверхности тела при развитии трещины, является константой данного материала, не зависящей от нагрузок, формы и размеров тела.
Следует отметить, что Ю.М. Мисник и К.А. Долгов сформулировали аналогичное для взрывного разрушения определение: «удельная поверхностная энергоемкость является физической константой породы, не зависящей от способа ее разрушения».
Согласно теории квазихрупкого разрушения для всех материалов при больших l и L наиболее вероятен случай, когда размер области пластической деформации d имеет свой предел (рис. 1.5). При больших l и L возможен единый энергетический подход к решению задачи разрушения породы.

В рамках теории квазихрупкого разрушения хрупкое есть предельное состояние при d→0, а пластическое при d→∞. Здесь d представляет собой область возможных пластических деформаций. Этим переходом от хрупкого к пластическому разрушению и их взаимодействию и интересна теория квазихрупкого разрушения.
В первом случае наличие двух положений d объясняет отрыв атомов и ионов, как механизм хрупкого разрушения, а во втором - при пластическом соскальзывании атомов с одного на другой уровень. С энергетической точки зрения, казалось бы, здесь требуется меньшее усилие при разрушении, но непрерывного скольжения атомов не происходит, так как дислокации постепенно выходят на края (поверхности) тела.
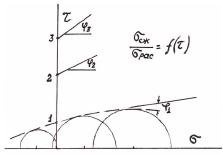
Основным постулатом для хрупкого разрушения является реализация теории наибольших нормальных напряжений (максимальных деформаций). Применительно к горным породам лучше подходит теория прочности Мора, основанная на зависимости между касательными и нормальными напряжениями. Рассматривая точку приложения усилий в сложнонапряженном состоянии, Mop представляет разрушение как совместное действие τ и σ. По теории Мора разрушение наступает при τ, превышающем предельное τраз, а его величина соответствует наибольшему нормальному напряжению σ. Построением кругов (напряжений) Мора в каждой точке, определением огибающей, устанавливается вязь между касательными и нормальными напряжениями:

где φ - угол внутреннего трения; с - сцепление.
Огибающая кругов Мора называется паспортом прочности горной породы. Если φ - угол внутреннего трения, то tgφ - есть коэффициент трения, а сцепление С является пределом прочности на срез при отсутствии нормальных напряжений. Угол φ характеризует степень связности, так как для связных пластичных пород (глины, суглинки) огибающая почти параллельна оси абсцисс, а для рыхлых (песок, гравий) начинается в начале координат.
Экспериментально установлено, что сцепление С зависит от соотношения σсж и σраст. С ростом отношения σсж/σраст увеличивается С и возрастает φ, а это означает и рост τ. Согласованное увеличение сопротивлений подтверждает правильность концепции М.М. Протодьяконова, введшего коэффициент крепости в предположении, что чем выше σсж у породы, тем выше и все остальные виды напряжений (σраст, σсдв и т.д.), очевидно, что это относится и к касательным напряжениям.
Кинетическая или термофлуктуационная теория разрушения С.Н. Журкова учитывает влияние на прочность твердого тела факторов температуры и времени действия нагрузки.
Замечено, что чем более длительное время нагрузки действуют на горную породу, тем меньше становятся упругие свойства (Е, μ и др.) и тем значительнее проявляются их пластические свойства.
При увеличении продолжительности действия напряжений (рис. 1.7) происходит постепенное снижение прочности горных пород. Такая прочность называется длительной σдл, это падение во времени не бесконечно, а достигает некоторого предела. Она значительно меньше стандартной прочности.

Зависимость прочности твердого тела от длительности воздействия нагрузки и температуры описывается уравнением Журкова:

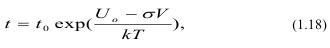
где t - время, требуемое для развития деформаций в породе до ее разрушения при напряжении σ;
tо - константа, совпадающая по порядку с периодом колебаний атомов и независящая от химического состава и структуры тела;
Uо - энергия активации процесса разрушения;
V - активационный объем процесса разрушения, зависящий от структуры тела и составляющий несколько атомных объемов;
k T - мера энергии тепловых флуктуаций.
Из уравнения следует, что энергия твердого тела составляет энергию колебательных движений частиц, закрепленных в кристаллической решетке. Сообщение им дополнительной тепловой энергии приводит к ослаблению межатомных связей, тогда разрушение твердого тела наступает при напряжениях, меньших теоретически вычисленных, т.е.:

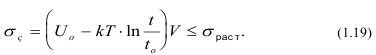
Кинетическая теория разрушения С.Н. Журкова построена на том, что разрушение не является критическим состоянием тела, поскольку в твердом теле происходит непрерывный процесс накопления повреждений (старение), которые приводят к полному его разрушению. Приложенные извне нагрузки и напряжения σр лишь уменьшают длительность существования тела в неразрушенном состоянии в соответствии с приведенным выше законом изменения времени t.
Возможное снижение прочности из-за старения вследствие развития дефектов и увеличения их количества, представленное в теории С.Н. Журкова, побудило В.H. Родионова выдвинуть несколько иную модель твердого тела, как сплошную идеальную среду. В ней, вероятно, равномерно распределены неоднородности разных размеров. На них концентрируются напряжения, приводящие к необратимым деформациям.
Напряжения внутри твердого тела состоят из упругих и локальных напряжений на неоднородностях. Изменение первых подчинено закону Гука, а вторые возникают при критических скоростях деформации.

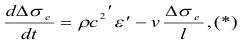
Механизм разрушения - это по существу представление о соотношении напряжений и деформаций, т.е. выражается уравнением состояния:
где Δσe — избыточное напряжение на неоднородности, размером l;
С — скорость поперечной волны;
ρ — плотность твердого тела;
ε' — скорость деформации сдвига;
v — скорость релаксации, т.е. падения Δσ при постоянной ε;
t — время воздействия на твердое тело.
Если t<1/v мало, то интеграл (*) выражается как:

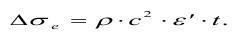
С ростом t сопротивление определится как:

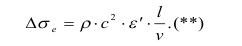
Это значит, что с ростом неоднородности и вообще разрушаемого объема тела (Vo), напряжения также будут расти при постоянной скорости деформации.
Если тело бесконечно велико, то в нем при любой скорости деформации всегда найдутся неоднородности достаточно большого размера, на которых избыточное напряжение приведет к разрушению. Размер такой неоднородности равен:

В формулировках закономерностей С.Н. Журкова постоянно прослеживается вероятностный исход в зависимости от встречи неоднородностей достаточного размера.
Обоснованию вероятностной концепции разрушения посвящена работа С.А. Гончарова, А.И. Дремина и др. Для использования формального математического аппарата имеются следующие основания.
1. Горные породы характеризуются изменчивостью прочностных свойств, вызываемой разнообразием минералогического состава, структурой, текстурой и трещиноватостью.
2. Прочность образцов горных пород зависит от их размеров, увеличение которых приводит к насыщению их различными дефектами, что при их испытании способствует уменьшению прочности. Условно можно считать, что при объеме образца 1 м3 отмечается максимальная насыщенность его дефектами и при дальнейшем увеличении размеров образца породы прочность не уменьшится. На самом деле это не совсем так, поскольку, если существуют различные уровни блочности, то и плотность дефектов разная.
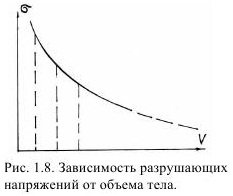
3. Физическая причина разрушения такой модели заключается в вероятности встречи в заданном объеме (рис. 1.8) опасного дефекта, которому соответствует определенная величина прочности, т.е. это констатация сущности статистической теории прочности.

Если распределение дефектов в объеме Vo подчинено нормальному закону Гаусса или Вейбулла (могут быть и другие виды распределения), а вероятность разрушения F(x), тогда вероятность неразрушения объема в m раз большего V составит:

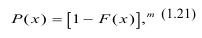
где m=V/Vo и для вероятности его разрушения имеем:

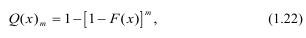
где Q(x)m - функция распределения прочности образца объемом V=Vo*m.
При m=50-100 Q(x)m стремится к распределению Гумбеля:

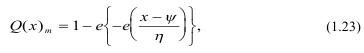
где φ и η — параметры положения и масштаба, определяемые как:

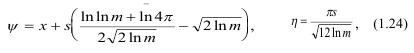
где S - среднеквадратическое отклонение прочности;
х - среднее значение прочности;
х - значение действующего напряжения.
Пример для расчета. При испытании образцов получены средние значения прочности на растяжение σр=15 МПа, среднеквадратическое отклонение S= 4,0 МПа.
Функция вероятности разрушения образцов испытуемого объема при напряжениях не больше х:

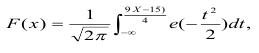
или вероятность разрушения при х=17 МПа составит:

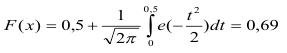
при

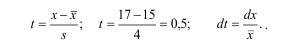
Если образец по размерам в пять раз больше испытанного при том же действующем напряжении х=17 МПа, по (1.2) имеем вероятность его разрушения:

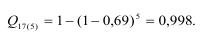
Если напряжение не больше х=9 МПа, то:

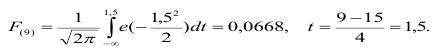
При том же напряжении, но если образец в 50 раз больше (m=50), имеем:

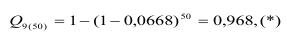
Используя распределение Гумбеля, применительно к тем же данным, получим:

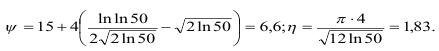
При х=9,0МПа:

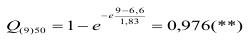
т.е. Q* и Q** отличаются менее чем на 1%.
Нормальный закон распределения не в полной мере отражает процесс, Гаусс не учитывает эксцесс и асимметрию, чего лишен закон Вейбулла, хорошо согласующийся с критерием разрушения Гриффитса:

где σ - разрушающее напряжение;
E - модуль упругости;
Us — энергия на единицу площади;
1 - полудлина трещины.
Так как трещин в породе много, они разные по размерам и распределены случайным и независимым образом, то прочность образца зависит от дефекта наибольших размеров. Тогда функция распределения плотности вероятности по Вейбуллу равна:

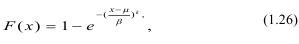
где х - текущее напряжение;
μ - крайняя левая граница прочности;
β - параметр масштабного фактора;
k - коэффициент однородности материала, принимающий значения 1/4.
Задача сводится к определению μ, β, k при известных S (среднеквадратичных отклонениях), а также асимметрии.
Коэффициент однородности определяется приравниванием теоретически вычисленного коэффициента асимметрии Aт и вычисленного Aг с учетом гамма-функции Г(х) вида:


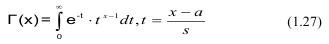
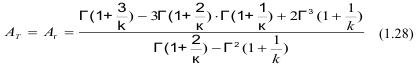
Из (1.28) определяется «к» и затем величина масштабного фактора β. Соотношение (1.28) решается итерациями на компьютере до Aг=μ3/S3.

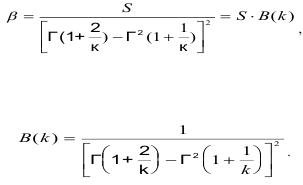
Значение крайнего левого предела соответствует:

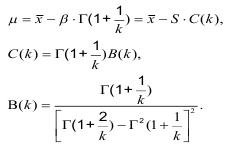
Приведем пример с ранее показанными данными.

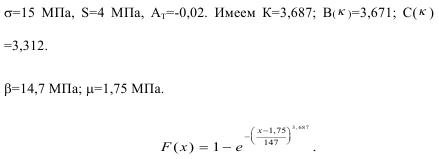
При х=9 МПа, F(x)=0,0712 и вероятность разрушения равна:

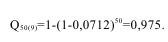
Сравнение полученного значения с ранее вычисленным значением вероятности свидетельствует об их равенстве.
Приведенные выше вычисления вероятности разрушения под действием указанных напряжений относятся к образцам с различными размерами и, следовательно, различной прочностью, что свидетельствуют об известном масштабном эффекте.
Проявление масштабного эффекта заключается в том, что с ростом энергии нагружения изменяется соотношение между размерами зон разрушения и размерами самой неоднородности, чем и характеризуется горная порода. Имеющиеся экспериментальные результаты показывают, что размер образца влияет на его прочность, о чем, собственно, и говорят вычисления при вероятностном подходе. Природа этого явления определяется в основном статистическими причинами, т.е. в большем объеме больше вероятность присутствия дефектов.
Однако эта связь выполняется до определенного предела, пока число дефектов на единицу объема образца не достигнет предельной величины, характерной для данной породы. Прочность изменяется с объемом в соответствии с соотношением:

где m=12 для прочности на сжатие и m=6 - при растяжении.
Таким образом, получается, что при сжатии зависимость прочности от объема более слабая. Это можно объяснить тем, что часть дефектов находится в зажатом состоянии и не развивается. При растяжении, наоборот, поле напряжений способствует развитию дефектов.
Возникает вопрос, а каким является предельный размер образца, когда начинает падать прочность? Анализ показывает, что он составляет около 10 см, т.е. соответствует размеру образца, или несколько его превышает.
При одноосном растяжении разрушение агрегата, например, трещиноватого массива с элементами различной прочности, рассматривается как разрушение наиболее слабого элемента из всего их многообразия соединенных последовательно. Прочность такого агрегата оказывается переменной и зависящей от объема:

где n - число элементов (блочность массива); А - константа.
При трехосном сжатии разрушение аналогичного агрегата рассматривается уже как одновременное разрушение параллельно соединенных элементов. Такая концепция означает, что прочность агрегата не зависит от объема образца и равна средней прочности элементов.

---