Удельная потенциальная энергия в единице объема горной породы

Из курса физики известно, что потенциальная энергия U1 тела массой m, находящегося на поверхности, относительно центра Земли, оценивается в ее абсолютном значении формулой

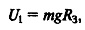
где R3 — радиус Земли, м.
Тело такой же массы, расположенное ниже уровня поверхности на глубине Н, обладает относительно центра Земли меньшей потенциальной энергией U2:

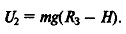
Примем за исходный (нулевой) энергетический уровень поверхность Земли. Тогда потенциальная энергия тела, находящегося на поверхности, относительно энергетического уровня, определяемого глубиной H, будет

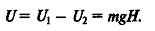
Примем массу m за величину, заключенную в единице объема V. Тогда уравнение (11.5) примет вид

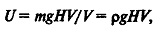
где ρ — плотность вещества, кг/м3.
Анализируя уравнение (11.8), приходим к выводу, что удельная потенциальная энергия сил гравитации ur (Дж/м3) представлена выражением ur=ρgH, т. е. можно записать

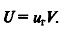
Объем V относится к массе тела m, находящегося на поверхности Земли, а величина потенциальной энергии определяется относительно уровня на глубине Н. Однако можно также показать, что потенциальная энергия тела массой m, находящегося на поверхности относительно уровня Н, имеет такую же потенциальную энергию U, как масса М столба пород высотой Н относительно уровня Н+h.
На рис. 11.3 в массиве пород выделена призма (столб), имеющая поперечное сечение s=h2 и высоту Н.

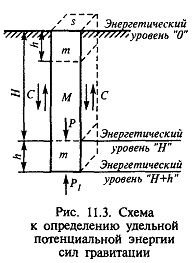
В основании призмы и у поверхности выделено два единичных объема V=h3=sh, которые имеют одинаковые массы m=ρV. Выделенная нами призма находится в статическом равновесии с окружающим ее массивом благодаря реакции опоры P1 и сил сцепления С по ее граням.
Потенциальная энергия призмы, которая имеет массу М, относительно уровня Н+h будет

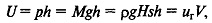
где ρ — средняя плотность пород призмы.
Поскольку V=sh является малым объемом в основании призмы, то uг — удельная потенциальная энергия, накопленная силами гравитации в этом объеме. Нами не учтена собственная потенциальная энергия массы m, находящейся в основании призмы, которая равна Um=ρghV/2. Однако при h=1 м, H=100 м величина этой энергии составит 0,5% энергии U. Поэтому при Н>h энергией Um можно пренебречь или всю потенциальную энергию следует относить к центру объема V.
Если вместо объема V, представляющего собой опору призмы, образовать полость (выработку) такого же объема, то призма (столб породы) зависнет благодаря силам сцепления С (см. рис. 11.3). Однако потенциальная энергия этого столба, согласно закону сохранения энергии, не исчезнет, так же, как не исчезнет вес Р выделенной нами призмы. Поэтому потенциальная энергия, определяемая уравнением (11.9), является той дополнительной удельной энергией, которая будет сосредоточена вокруг полости (выработки).

---