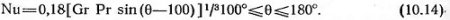Моделирование геотехнологических процессов (часть 3)

Чтобы избежать вычислений бесконечных рядов, целесообразно аппроксимировать показатель степени таким образом, чтобы решение системы уравнений (10.10) не содержало рядов. Это возможно, если n=m/(1+m). Здесь m — целое число.
Концентрация полезного компонента С в жидкой фазе определяется выражением

где β — постоянная.
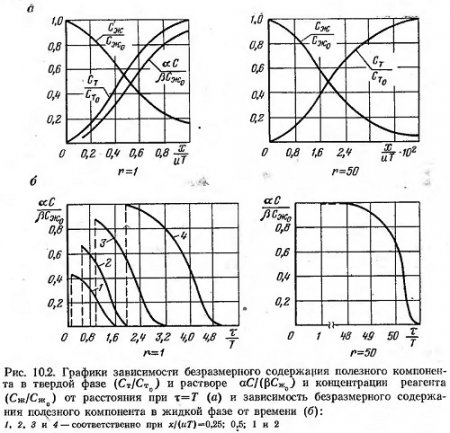
Соответствующие искомые зависимости, полученные из решения системы уравнений (10.10) для m=1 представлены на рис. 10, 2, а, б.

Характер их определяется главным образом параметром η, причем при η>1 существует некоторый временной интервал, в течение которого содержание полезного компонента в отбираемом растворе практически постоянно.
Физическое моделирование геотехнологического процесса можно рассмотреть на примере подземного растворения солей. Обычно экспериментальные исследования проводятся на природных образцах соли. Уравнение, связывающее определяемые величины с влияющими факторами, необходимо искать в виде зависимости от критериев Пекле, Фруда и Прандтля. Таким образом, используя природные материалы, диапазоны температур и краевые условия, идентичные натурным, возможность моделирования определяем соблюдением чисел подобия Ре (Rе) и Fr. Для области свободной конвекции эта возможность зависит от соблюдений числа Грасгофа (Сr=АrRе2), откуда сразу следует, что при геометрических масштабах, отличных от 1, подобие обеспечить не удается. Исследованиями ВНИИГа было показано, что приближенное подобие обеспечивает удовлетворительные для практики результаты. Исследования на моделях позволили выявить гидродинамическую схему потоков в камере растворения. Установлено наличие двух независимых видов потоков. Потоки одного вида вызваны всплыванием и растеканием вдоль потолка камеры вводимого растворителя, а потоки другого вида — перемещением рассола в соответствии с его плотностью.
Одним из основных показателей, лежащих в основе проектных расчетов, является средняя радиальная скорость растворения соли. Она является функцией концентрации растворителя, его температуры, наклона поверхности растворения и других факторов.
В критериальном виде эти зависимости имеют вид

при углах наклона поверхности растворения 0<90º

Уравнения справедливы при свободно-конвективном растворении соли в турбулентном режиме.
Примером приближенного физического моделирования может служить экспериментальное изучение процесса подземной выплавки серы, представляющих собой исключительно сложное явление, характеризуемое гидродинамическими процессами течения двух несмешивающихся жидкостей — горячей воды и жидкой серы в зоне плавления, вытеснением горячей водой, холодной пластовой жидкости вне зоны плавления, процессами теплопереноса в пласте, наличием подвижных границ зон плавления, фазовым переходом твердой серы в жидкое состояние и др.
На основании полученной системы критериев подобия видно, что подобрать параметры модели, обеспечивающие равенство критериев натуры и модели, практически невозможно.
Например, анализ полученных критериев подобия показал, что, если основное значение имеют внешние гидродинамические силы и тепловые процессы, время протекания процессов пропорционально квадрату линейного масштаба при равенстве свойств модели и натуры. При этом подобие процессов массопереноса, обусловленное гравитационными силами, не соблюдается.
Исходной при проектных расчетах служит зависимость количества продукции, добываемой из скважин, от времени ее отработки при различных расходах рабочих агентов, сеток скважин и других параметрах в различных горно-геологических условиях.